Improper integral

Improper integrals are unrestricted in one direction. They are used to calculate areas that extend to infinity.

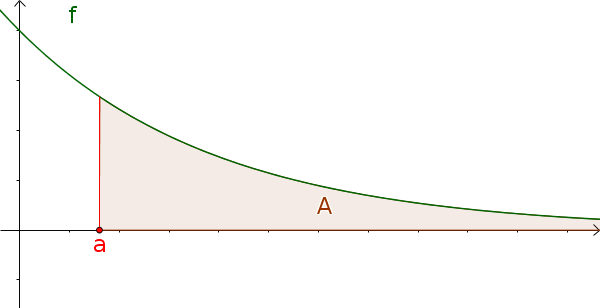
The area has only one limit and goes in the other direction to infinity.

Examples

Examples of improper integrals are therefore

• $\int_a^\infty f(x)\,\mathrm{d}x$


• $\int_{-\infty}^b f(x)\,\mathrm{d}x$

When calculating, the infinity is first replaced by a variable $k$ to calculate the given integral. Then you form the limit of the result.

Example

$\int_1^\infty \frac1{x^2}\,\mathrm{d}x$

1. Definite integral with $k$ instead of $\infty$

   We replace the limit with $\infty$ by $k$ and thereby obtain a definite integral, which we can solve in step 2.

   $\int_1^k \frac1{x^2}\,\mathrm{d}x$

2. Determine definite integral

   Now we determine the integral like a normal definite integral, where we have $k$ and no number.

   $\int_1^k \frac1{x^2}\,\mathrm{d}x$ $=[-\frac1x]_1^k$ $=F(k)-F(1)$ $=-\frac1k - (-\frac11)$ $=\color{red}{-\frac1k+1}$

3. Determine limit

   Now we can let $k$, which should be infinite, run against $\infty$.

   For this we use the limit

   $\lim\limits_{k\to\infty}\int_1^k \frac1{x^2}\,\mathrm{d}x$ $=\lim\limits_{k\to\infty}(\color{red}{-\frac1k+1})$

   We think: What if the number $k$ would become very large or infinite? 1 divided by a very large number keeps approaching zero. So:

   $\lim\limits_{k\to\infty}(\color{red}{-\frac1k+1})$ $=0+1$ $=1$

   The area from 1 to infinity is approaching the number 1 in the case of the function $\frac1{x^2}$. The area is therefore finite (the area is not infinitely large).