Uneigentliches Integral
Uneigentliche Integrale sind in eine Richtung unbeschränkt. Sie dienen zum Berechnen von Flächen, die sich bis ins Unendliche ausdehnen.
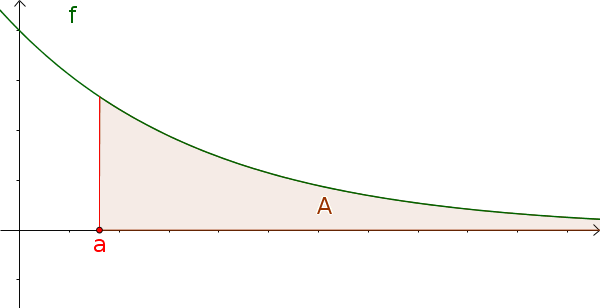
Die Fläche hat nur eine Grenze und geht in die andere Richtung ins Unendliche.
Beispiele
Beispiele für uneigentliche Integrale sind daher
- $\int_a^\infty f(x)\,\mathrm{d}x$
- $\int_{-\infty}^b f(x)\,\mathrm{d}x$
Info
Beim Berechnen wird zuerst das Unendlich durch eine Variable $k$ ersetzt, um das bestimmte Integral berechnen zu können. Anschließend bildet man den Grenzwert des Ergebnisses.
Vorgehensweise
- $\infty$ durch $k$ ersetzen
- Bestimmtes Integral berechnen
- Grenzwert bestimmen
Beispiel
$\int_1^\infty \frac1{x^2}\,\mathrm{d}x$
-
Bestimmtes Integral mit $k$ statt $\infty$
Wir ersetzen die Grenze mit $\infty$ durch $k$ und erhalten dadurch ein bestimmtes Integral, das wir in Schritt 2 lösen können.$\int_1^k \frac1{x^2}\,\mathrm{d}x$
-
Bestimmtes Integral berechnen
Nun berechnen wir das Integral wie ein normales bestimmtes Integral, wobei wir hier $k$ und keine Zahl haben.$\int_1^k \frac1{x^2}\,\mathrm{d}x$ $=[-\frac1x]_1^k$ $=F(k)-F(1)$ $=-\frac1k - (-\frac11)$ $=\color{red}{-\frac1k+1}$
-
Grenzwert bestimmen
Jetzt können wir $k$, das unendlich sein soll, gegen $\infty$ laufen lassen.Dazu nutzen wir den Grenzwert
$\lim\limits_{k\to\infty}\int_1^k \frac1{x^2}\,\mathrm{d}x$ $=\lim\limits_{k\to\infty}(\color{red}{-\frac1k+1})$
Wir überlegen uns: Was wäre, wenn die Zahl $k$ ganz groß bzw. unendlich werden würde. 1 durch eine sehr große Zahl nähert sich immer weiter der Null. Also:
$\lim\limits_{k\to\infty}(\color{red}{-\frac1k+1})$ $=0+1$ $=1$
Der Flächeninhalt von 1 bis unendlich nähert sich bei der Funktion $\frac1{x^2}$ immer weiter der Zahl 1. Der Flächeninhalt ist also endlich (die Fläche ist nicht unbegrenzt groß).
Merke
$\lim\limits_{k\to\infty}\int_a^k f(x)\,\mathrm{d}x$,
dann bezeichnet man diesen als uneigentliches Integral und schreibt dafür
$\int_a^\infty f(x)\,\mathrm{d}x$.
