Mathe ↠ Anwendung Integralrechnung ↠ Rotationsvolumen

Rotationsvolumen

Eine weitere Anwendung der Integralrechnung ist das Berechnen von Rotationsvolumen.

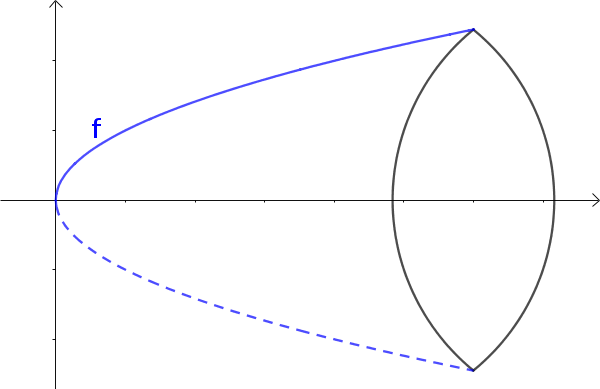
Der Rotationskörper wird beschrieben durch eine Funktion $f$ und rotiert um die x-Achse. Das Volumen des Körpers lässt sich mit einem Integral berechnen.

Die Formel lautet

$V=\pi\cdot \int_a^b (f(x))^2\,\mathrm{d}x$
i

Vorgehensweise

  1. Funktion quadrieren
  2. Einsetzen und Integral berechnen

Beispiel

Die Fläche unter dem Funktionsgraph von $f(x)=\sqrt{x}$ rotiert im Intervall $[0; 6]$ um die x-Achse. Berechne das Rotationsvolumen.

  1. Funktion quadrieren

    Da in der Formel $(f(x))^2$ vorkommt, sollte man dies zur Übersichtlichkeit vorher machen.

    $(f(x))^2$ $=(\sqrt{x})^2$ $=x$

  2. Einsetzen und Integral berechnen

    Die gegebenen Integrationsgrenzen 0 und 6 sowie die quadrierte Funktion einsetzen.

    $V=\pi\cdot \int_a^b (f(x))^2\,\mathrm{d}x$

    $V=\pi\cdot \int_0^6 x \,\mathrm{d}x$

    Bestimmtes Integral berechnen

    $=\pi\cdot [\frac12 x^2]_0^6$ $=\pi \cdot 18$ $\approx56,55$

    Das Volumen beträgt ca. 56,55 VE.