Math ↠ Application integral calculus ↠ Volume of a solid of revolution

Volume of a solid of revolution

Another application of integral calculus is the calculation of the volume of a solid of revolution.

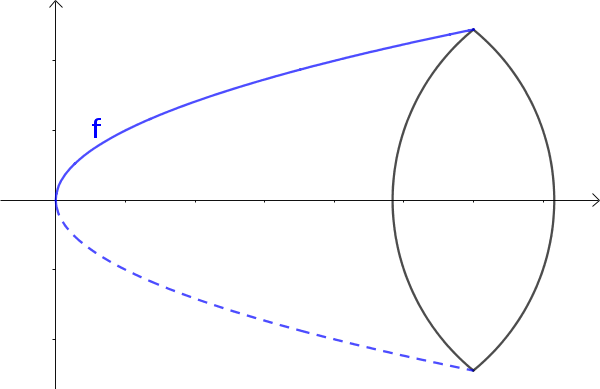
The solid of revolution is described by a function $f$ and rotates around the x-axis. The volume of the solid figure can be calculated with an integral.

The formula is

$V=\pi\cdot \int_a^b (f(x))^2\,\mathrm{d}x$
i

Method

  1. Square the function
  2. Insert and calculate integral

Example

The area under the function graph of $f(x)=\sqrt{x}$ rotates around the x-axis in the interval $[0; 6]$. Calculate the volume of the solid of revolution.

  1. Square the function

    Since $(f(x))^2$ occurs in the formula, you should do this for clarity beforehand.

    $(f(x))^2$ $=(\sqrt{x})^2$ $=x$

  2. Insert and calculate integral

    Insert the given limits of integration 0 and 6 as well as the squared function.

    $V=\pi\cdot \int_a^b (f(x))^2\,\mathrm{d}x$

    $V=\pi\cdot \int_0^6 x \,\mathrm{d}x$

    Determine definite integral

    $=\pi\cdot [\frac12 x^2]_0^6$ $=\pi \cdot 18$ $\approx56.55$

    The volume is approximately 56.55 VU.