Вычисление объема тела вращения

Интеграл, также применяется при вычислении объема тела вращения.

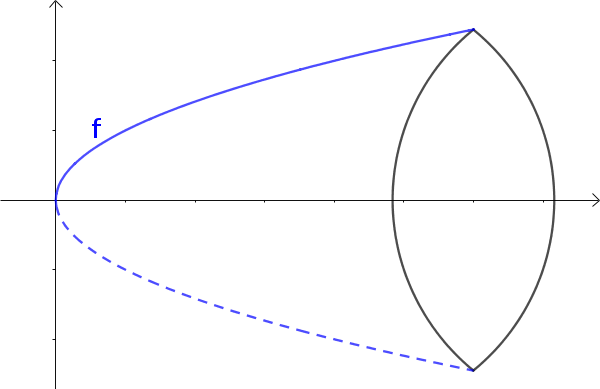
Тело вращения, описанно функцией $f$ и вращается вокруг оси X. Объем фигуры можно рассчитать с помощью интеграла.

Формула:

Например

Область под графиком функции $f(x)=\sqrt{x}$ вращается вокруг оси x в интервале $[0; 6]$. Вычислите объем тела вращения.

1. Возведите функцию в квадрат

   Поскольку для функции $(f(x))^2$, применима формула, вы должны сделать это заранее.

   $(f(x))^2$ $=(\sqrt{x})^2$ $=x$

2. Подставьте и рассчитайте интеграл

   Подставьте заданные пределы интегрирования 0 и 6, а также квадратную функцию.

   $V=\pi\cdot \int_a^b (f(x))^2\,\mathrm{d}x$

   $V=\pi\cdot \int_0^6 x \,\mathrm{d}x$

   Найдите определенный интеграл

   $=\pi\cdot [\frac12 x^2]_0^6$ $=\pi \cdot 18$ $\approx56.55$

   Объем тела вращения 56.55 VU.