Несобственный интеграл

Несобственные интегралы не имеют ограничения в одном направлении. Они используются для расчета площадей, которые простираются до бесконечности.

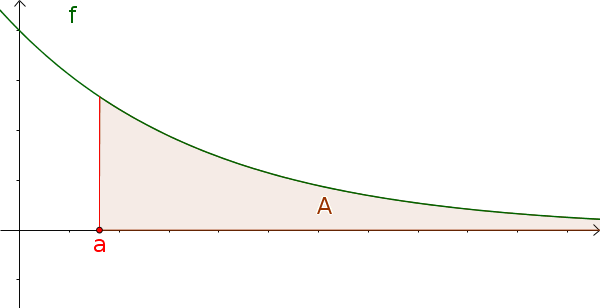
Область имеет только один предел и стремится в другом направлении к бесконечности.

Например

Примерами несобственных интегралов являются:

• $\int_a^\infty f(x)\,\mathrm{d}x$


• $\int_{-\infty}^b f(x)\,\mathrm{d}x$

При вычислении, бесконечность, сначала заменяют переменной $k$ для вычисления данного интеграла, затем вы находите предел. .

Например

$\int_1^\infty \frac1{x^2}\,\mathrm{d}x$

1. Определенный интеграл с переменной $k$ вместо $\infty$

   Мы заменяем предел $\infty$ на $k$ и тем самым мы находим определенный интеграл, который нам понадобится во 2 пункте.

   $\int_1^k \frac1{x^2}\,\mathrm{d}x$

2. Найдите определенный интеграл

   Теперь мы определяем интеграл, как обычный определенный интеграл, где мы имеем $k$ без числа.

   $\int_1^k \frac1{x^2}\,\mathrm{d}x$ $=[-\frac1x]_1^k$ $=F(k)-F(1)$ $=-\frac1k - (-\frac11)$ $=\color{red}{-\frac1k+1}$

3. Определите предел

   теперь мы можем позволить $k$, которая должна быть бесконечной, обратиться против $\infty$.

   Для этого мы используем предел

   $\lim\limits_{k\to\infty}\int_1^k \frac1{x^2}\,\mathrm{d}x$ $=\lim\limits_{k\to\infty}(\color{red}{-\frac1k+1})$

   Мы думаем, а что, если число к будет очень большим или бесконечным? 1 деленная на очень большое число,продолжает стремиться к нулю. Так:

   $\lim\limits_{k\to\infty}(\color{red}{-\frac1k+1})$ $=0+1$ $=1$

   Область от 1 до бесконечности приближается к числу 1 в случае функции $\frac1{x^2}$. Таким образом, эта область имеет конец (она не бесконечна).