Graphen von Funktionen

Funktionen können wie Zuordnungen in einem Koordinatensystem graphisch dargestellt werden.

Jedes zur Funktion gehörige Zahlenpaar bestimmt einen Punkt im Koordinatensystem. Die Menge aller Punkte bezeichnet man als Funktionsgraphen.

Merke

Die Reihenfolge der Werte eines Punktes $P(x|y)$ ist wichtig. Merke: immer zuerst x, dann y.

Beispiel

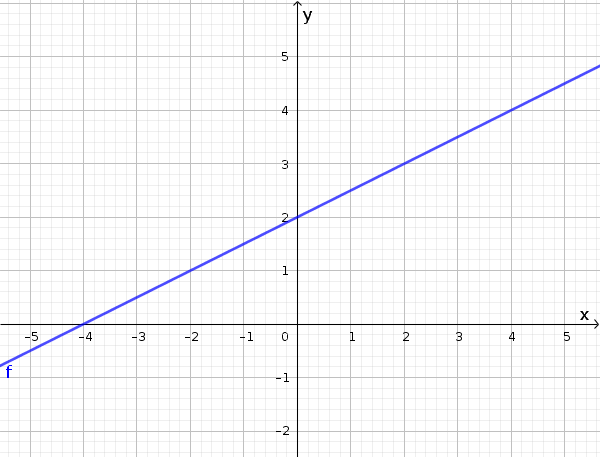
Gegeben sei die Funktion $f(x)=\frac12x+2$.

Wenn die Definitionsmenge lautet $D=\{-4,-2,0,2,4\}$, dann besteht der Graph nur aus den fünf Punkten $(-4|0)$, $(-2|1)$, $(0|2)$, $(2|3)$ und $(4|4)$.

$Funktionsgraph sind mehrere Punkte$

Wenn die Definitionsmenge aber alle rationalen Zahlen beinhaltet $D=\mathbb{Q}$, dann hat der Graph unendlich viele Punkte und ist daher eine Gerade:

$Funktionsgraph ist eine Gerade$

Tipp

Verwechsle nicht den Graphen einer Funktion mit der Funktion selbst! Das sind zwei unterschiedliche Begriffe.

Funktionsgraphen erkennen

Eine Funktion ist eine eindeutige Zuordnung, also wird jedem x- genau ein y-Wert zugeordnet.

Wie kann nun erkannt werden, ob es sich bei einem Graphen um einen Funktionsgraphen handelt oder nicht?

Merke

Der Graph einer Funktion kann niemals Punkte besitzen, die senkrecht übereinander liegen.

Beispiele

Ein gültiger Funktionsgraph wäre also:

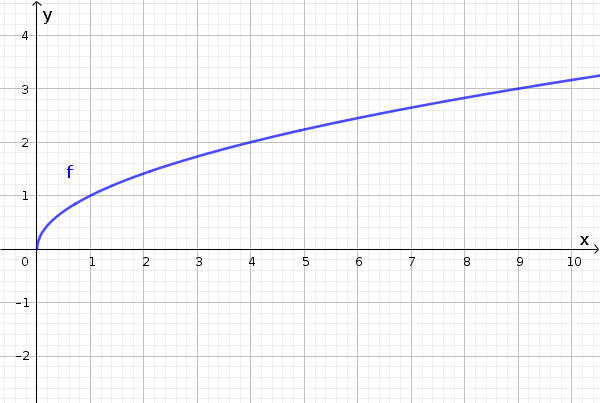
$Gültiger Funktionsgraph$

Kein Funktionsgraph ist allerdings folgender, da den x-Werten zwei y-Werte zugeordnet werden.

$Kein Funktionsgraph$