Graph of a function

Functions can be graphically displayed in a coordinate system just like relations.

Each pair of numbers belonging to the function determines a point in the coordinate system. The set of all points is called the graph of a function.

Remember

The order of the value of an ordered pair $(x|y)$ is important. Remember: x is always first, and then y.

Example

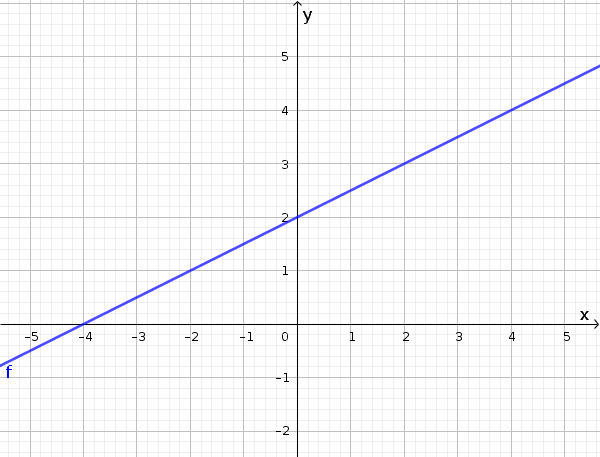
Given is the following function $f(x)=\frac12x+2$.

If the domain is $D=\{-4,-2,0,2,4\}$, then the graph only consists of five points $(-4|0)$, $(-2|1)$, $(0|2)$, $(2|3)$ and $(4|4)$.

$Funktionsgraph sind mehrere Punkte$

If the domain includes all rational numbers $D=\mathbb{Q}$, then the graph has an infinite amount of ordered pairs and thus forms a line:

$Funktionsgraph ist eine Gerade$

Hint

Do not mistake the graph of a function with the function itself! Those are two diffrent terms.

Recognizing a graph of a function

A function is a clear allocation of points, so each x-value is assigned to exactly one y-value.

How can it be recognized whether a graph is a graph of a function or not?

Remember

The graph of a function can never contain points which are vertically one above the other.

Example

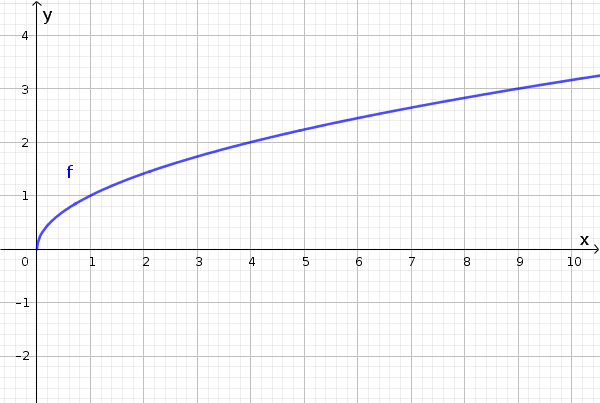
A valid graph of a function would be:

$Gültiger Funktionsgraph$

The following example is not a graph of a function, because the x-values are assigned to two y-values.

$Kein Funktionsgraph$