Математика ↠ Семейство кривых ↠ Кривая локуса

Кривая локуса

Экстремумы или точки перегиба графиков функции, семейства кривых лежат на новом графике, кривой локуса.

i

Подсказка

В общем случае, локас - это множество точек, удовлетворяющих некоторое условие.
!

Запомните

В этом случае кривая локуса является новой функцией, на графике которой есть определенные точки (например, экстремум или точка перегиба) из каждой функции семейства кривых.

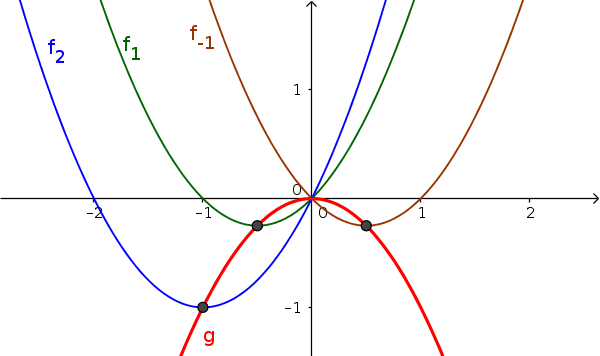
На рисунке: все минимумы семейства кривых $f_a$ лежат на графике новой функции $g$.
i

Метод

  1. Вычислите точки (например, экстремумы или точки перегиба)
  2. Составьте уравнение для x и y значений
  3. Переставьте уравнение для значения х и вставьте

Например

Определите все минимумы функции $f_a(x)=x^2+ax$ ($a\in\mathbb{R}$)

  1. Найдите производную

    $f_a(x)=x^2+ax$
    $f_a'(x)=2x+a$
    $f_a''(x)=2$

  2. Вычислите минимум

    вычислите экстремумы: приравняйте первую производную к нулю
    $f_a'(x)=0$
    $2x+a=0\quad|-a$
    $2x=-a\quad|:2$
    $x_E=-\frac{a}2$

    используйте предполагаемые точки для экстремумов во втором тесте:
    $f_a''(-\frac{a}2)=2>0$ => минимум

    вычислите y-координату и укажите минимум:
    $f_a(-\frac{a}2)$ $=(-\frac{a}2)^2+a\cdot(-\frac{a}2)$ $=\frac{a^2}4-\frac{a^2}2$ $=\frac{a^2}4-\frac{2a^2}4$ $=-\frac{a^2}4$

    $T(-\frac{a}2|-\frac{a^2}4)$

  3. Составьте уравнение для x и y значений

    из координат минимума теперь можно составить два уравнения
    $T(-\frac{a}2|-\frac{a^2}4)$
    $x=-\frac{a}2$
    $y=-\frac{a^2}4$

  4. Переставьте уравнение и вставьте

    уравнение для x теперь изменено на параметр $a$ и вставлено во второй.
    $x=-\frac{a}2\quad|\cdot(-2)$
    $a=-2x$

    $y=-\frac{a^2}4$
    $y=-\frac{(-2x)^2}4$ $=-\frac{4x^2}4$ $=-x^2$

    функция всех минимумов: $y=-x^2$