Ortskurve
Die Extrem- oder Wendepunkte aller Funktionsgraphen einer Funktionenschar liegen auf einem neuen Graphen, der Ortskurve.
!
Merke
Die Ortskurve ist eine neue Funktion, auf deren Graph jeweils ein bestimmter Punkt (z.B. Extrem- oder Wendepunkt) von jeder Funktion einer Schar liegt.
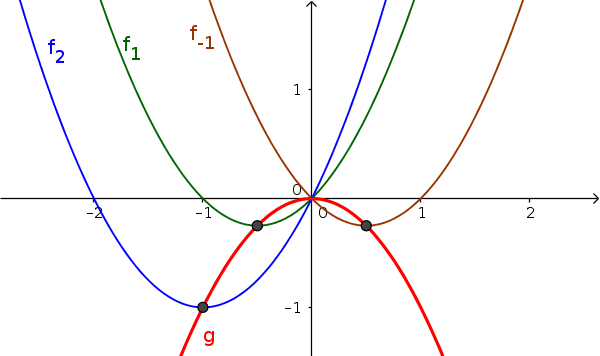
Zum Bild: Alle Tiefpunkte der Funktionen der Schar $f_a$ liegen auf dem Graphen der Ortskurve $g$.
i
Vorgehensweise
- Gesuchte Punkte (z.B. Extrem- oder Wendepunkte) berechnen
- Gleichungen für x- und y-Wert aufstellen
- Gleichung mit x-Wert umstellen und einsetzen
Beispiel
Bestimme die Ortskurve der Tiefpunkte von $f_a(x)=x^2+ax$ ($a\in\mathbb{R}$)
-
Ableitungen bestimmen
$f_a(x)=x^2+ax$
$f_a'(x)=2x+a$
$f_a''(x)=2$ -
Tiefpunkt berechnen
Extrempunkte berechnen: Erste Ableitung gleich Null setzen
$f_a'(x)=0$
$2x+a=0\quad|-a$
$2x=-a\quad|:2$
$x_E=-\frac{a}2$
extremwertverdächtige Stellen in die zweite Ableitung einsetzen:
$f_a''(-\frac{a}2)=2>0$ => Tiefpunkt
y-Koordinate berechnen und Tiefpunkt angeben:
$f_a(-\frac{a}2)$ $=(-\frac{a}2)^2+a\cdot(-\frac{a}2)$ $=\frac{a^2}4-\frac{a^2}2$ $=\frac{a^2}4-\frac{2a^2}4$ $=-\frac{a^2}4$
$T(-\frac{a}2|-\frac{a^2}4)$ -
Gleichungen für x- und y-Wert aufstellen
Aus den Koordinaten des Tiefpunktes kann man nun zwei Gleichungen aufstellen.
$T(-\frac{a}2|-\frac{a^2}4)$
$x=-\frac{a}2$
$y=-\frac{a^2}4$ -
Gleichung umstellen und einsetzen
Die Gleichung für x wird jetzt nach dem Parameter $a$ umgestellt und in die zweite eingesetzt.
$x=-\frac{a}2\quad|\cdot(-2)$
$a=-2x$
$y=-\frac{a^2}4$
$y=-\frac{(-2x)^2}4$ $=-\frac{4x^2}4$ $=-x^2$
Ortskurve: $y=-x^2$
