Math ↠ Family of curves ↠ Locus curve

Locus curve

The extrema or inflection points of all function graphs of a family of curves lie on a new graph, the locus curve.

i

Info

In general, locus is a set of points satisfying some condition.
!

Remember

In this case, the locus curve is a new function, on whose graph there is a specific point (e.g. extrema or inflection point) of each function of the family of curves.

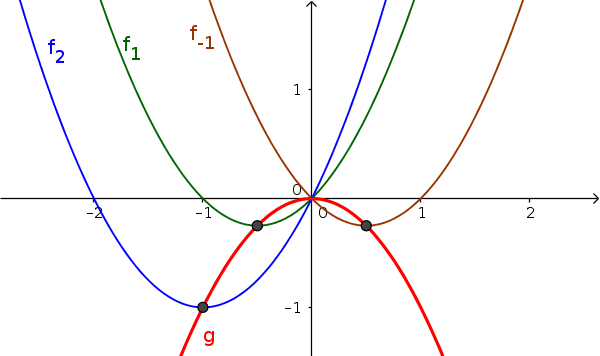
The picture: All minima of the family of curves $f_a$ lie on the graph of a new function $g$.
i

Method

  1. Calculate searched points (e.g. extrema or inflection points)
  2. Set up equations for x and y values
  3. Rearrange equation for x-value and insert

Example

Determine the function of all minima of $f_a(x)=x^2+ax$ ($a\in\mathbb{R}$)

  1. Find derivative

    $f_a(x)=x^2+ax$
    $f_a'(x)=2x+a$
    $f_a''(x)=2$

  2. Calculate minimum

    calculate extrema: Set first derivative equal to zero
    $f_a'(x)=0$
    $2x+a=0\quad|-a$
    $2x=-a\quad|:2$
    $x_E=-\frac{a}2$

    use suspicious points for extrema in the second derivative test:
    $f_a''(-\frac{a}2)=2>0$ => minimum

    calculate the y-coordinate and specify the minimum:
    $f_a(-\frac{a}2)$ $=(-\frac{a}2)^2+a\cdot(-\frac{a}2)$ $=\frac{a^2}4-\frac{a^2}2$ $=\frac{a^2}4-\frac{2a^2}4$ $=-\frac{a^2}4$

    $T(-\frac{a}2|-\frac{a^2}4)$

  3. Set up equations for x and y values

    from the coordinates of the minimum you can now set up two equations
    $T(-\frac{a}2|-\frac{a^2}4)$
    $x=-\frac{a}2$
    $y=-\frac{a^2}4$

  4. Rearrange equation and insert

    the equation for x is now changed to the parameter $a$ and inserted into the second one.
    $x=-\frac{a}2\quad|\cdot(-2)$
    $a=-2x$

    $y=-\frac{a^2}4$
    $y=-\frac{(-2x)^2}4$ $=-\frac{4x^2}4$ $=-x^2$

    function of all minima: $y=-x^2$