Common Point

When all functions of a family of curves go through a common point, a bundle of functions occurs.

Remember

Not every family of curves has a common point.

Hint

If there is a common intersection of all of the families function graphs, then there must be a location $x$ where the additional parameter disappears.
The intersection is therefore at this x-value.

Example

$f_a(x)=x^2+ax$ (with $a\in\mathbb{R}$)

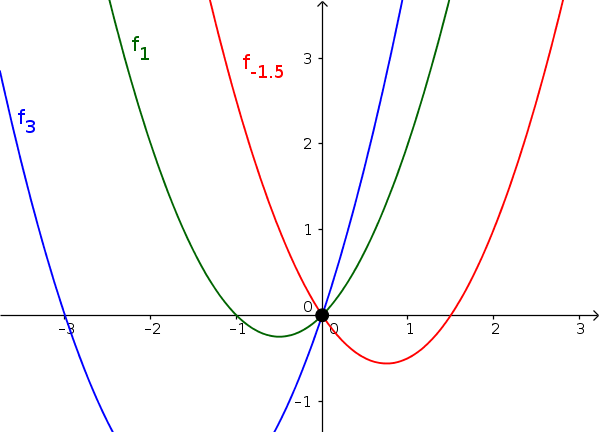
$\color{blue}{f_3(x)=x^2+3x}$
$\color{green}{f_1(x)=x^2+x}$
$\color{red}{f_{-1.5}(x)=x^2-1.5x}$

For $f(0)=0^2+a\cdot0=0$, the parameter $a$ is eliminated at $x=0$. Therefore, the family of curves has a common point at $(0|0)$.