Gemeinsamer Punkt

Ein Funktionenbündel liegt vor, wenn alle Funktionen einer Funktionenschar durch einen gemeinsamen Punkt gehen.

Merke

Nicht jede Funktionenschar besitzt einen gemeinsamen Punkt.

Tipp

Wenn ein gemeinsamer Schnittpunkt aller Funktionsgraphen der Schar vorhanden ist, dann muss es eine Stelle $x$ geben, an der der Scharparameter wegfällt.
Der Schnittpunkt liegt dann bei diesem x-Wert.

Beispiel

$f_a(x)=x^2+ax$ (mit $a\in\mathbb{R}$)

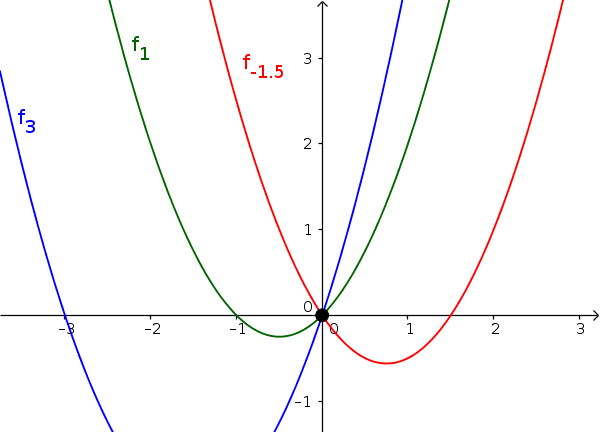
$\color{blue}{f_3(x)=x^2+3x}$
$\color{green}{f_1(x)=x^2+x}$
$\color{red}{f_{-1,5}(x)=x^2-1,5x}$

Für $f(0)=0^2+a\cdot0=0$ fällt der Scharparameter $a$ an der Stelle $x=0$ weg. Deshalb besitzt die Schar einen gemeinsamen Punkt bei $(0|0)$.