Funktionenschar
Eine Funktionenschar oder Kurvenschar ist eine Menge von Funktionen, die neben der Variable $x$ auch noch von einem weiteren Scharparameter abhängt.
Beispiel
Eine Funktionsgleichung $y=f(x)$ wird von einem Scharparameter abhängig, der mit der Funktion auf unterschiedliche Arten z.B. addiert oder multipliziert werden kann:
- $f_a(x)=f(x)+a$
- $f_b(x)=f(x+b)$
- $f_c(x)=c\cdot f(x)$
- $f_d(x)=f(d\cdot x)$
!
Merke
Für jeden Wert des Scharparameters erhält man einen eigenen Funktionsgraphen.
Beispiel
$f_a(x)=x^2+a$ (mit $a\in\mathbb{R}$)
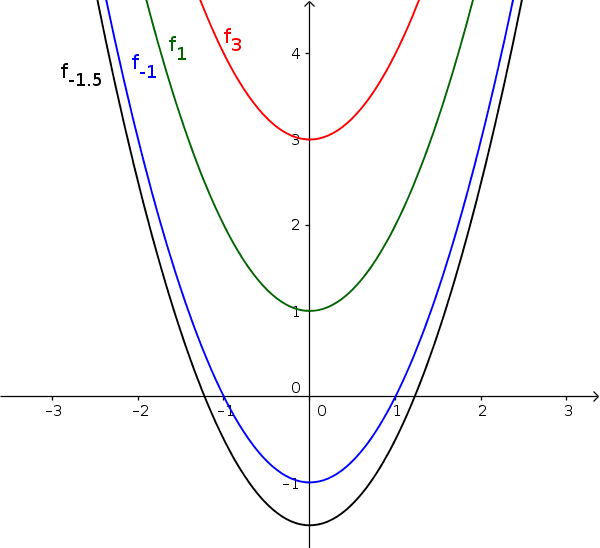
- $\color{red}{f_3(x)=x^2+3}$
- $\color{green}{f_1(x)=x^2+1}$
- $\color{blue}{f_{-1}(x)=x^2-1}$
- $\color{black}{f_{-1,5}(x)=x^2-1,5}$
