Правило пути

Второе правило пути: правило сложения

Например

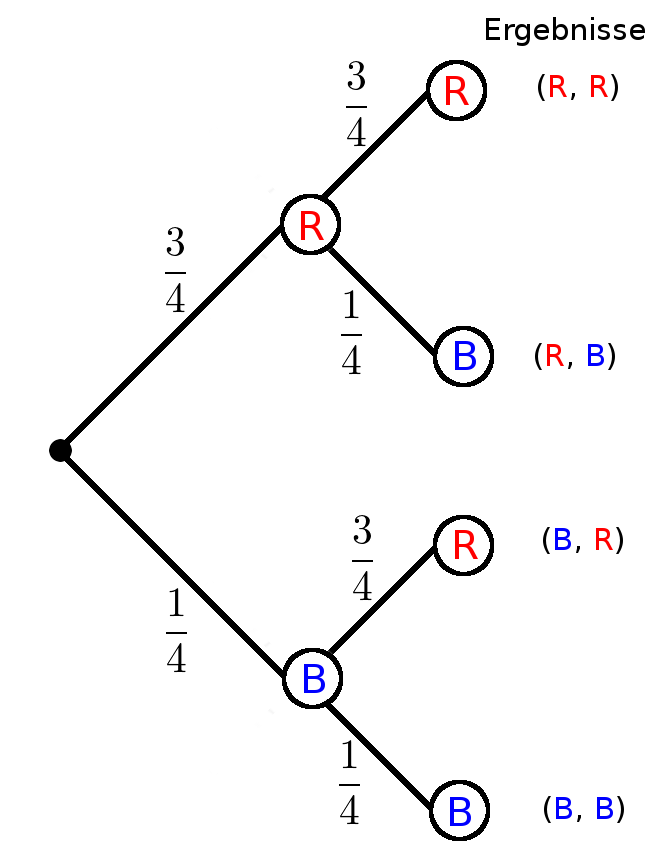
Вычислите вероятность красного и синего цветов вне зависимости от порядка.

1. Событие

   Повторение пространства выборки и события
   
   Пространство выборки:
   $\Omega=\{(R,R);(R,B);$ $(B,R);(B,B)\}$
   
   Событие:
   $E:\text{„красный и синий“}$
   $E=\{(R,B);(B,R)\}$

2. Правило умножения (первое правило пути)

   Вычислите вероятность отдельных исходов
   
   $P(R, B)=\frac34\cdot\frac14=\frac{3}{16}$
   $P(B, R)=\frac14\cdot\frac34=\frac{3}{16}$

3. Правило сложения (второе правило пути)

   Сложите вероятности.
   
   $P(E)$ $=P(R, B)+P(B, R)$ $=\frac{3}{16}+\frac{3}{16}$ $=\frac{6}{16}$