Math ↠ Tree Diagram ↠ 2nd path rule

Path rules

2nd path rule: Addition rule

!

Remember

The probability of an event corresponds to the sum of all associated path probabilities.

Example

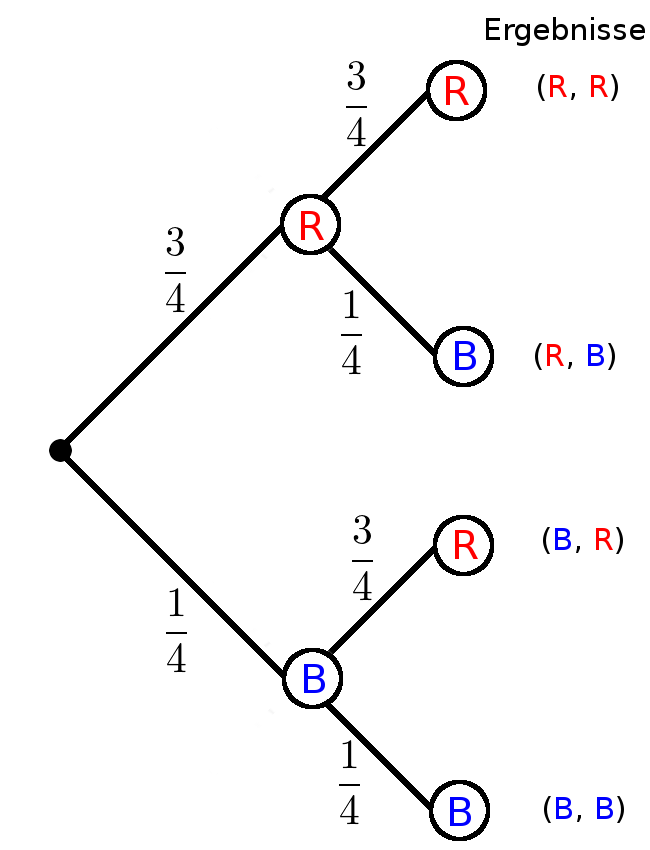
Calculate the probability of red and blue regardless of the order.

  1. Event

    Repetition of sample space and event

    Sample space:
    $\Omega=\{(R,R);(R,B);$ $(B,R);(B,B)\}$

    Event:
    $E:\text{„red and blue“}$
    $E=\{(R,B);(B,R)\}$

  2. Multiplication rule (1st path rule)

    Calculate the probabilities of the individual outcomes

    $P(R, B)=\frac34\cdot\frac14=\frac{3}{16}$
    $P(B, R)=\frac14\cdot\frac34=\frac{3}{16}$

  3. Addition rule (2nd path rule)

    Add up probabilities.

    $P(E)$ $=P(R, B)+P(B, R)$ $=\frac{3}{16}+\frac{3}{16}$ $=\frac{6}{16}$