Pfadregeln

2. Pfadregel: Summenregel

Beispiel

In einer Urne befinden sich 3 rote und 1 blaue Kugel. Es werden nacheinander 2 Kugeln mit Zurücklegen gezogen.

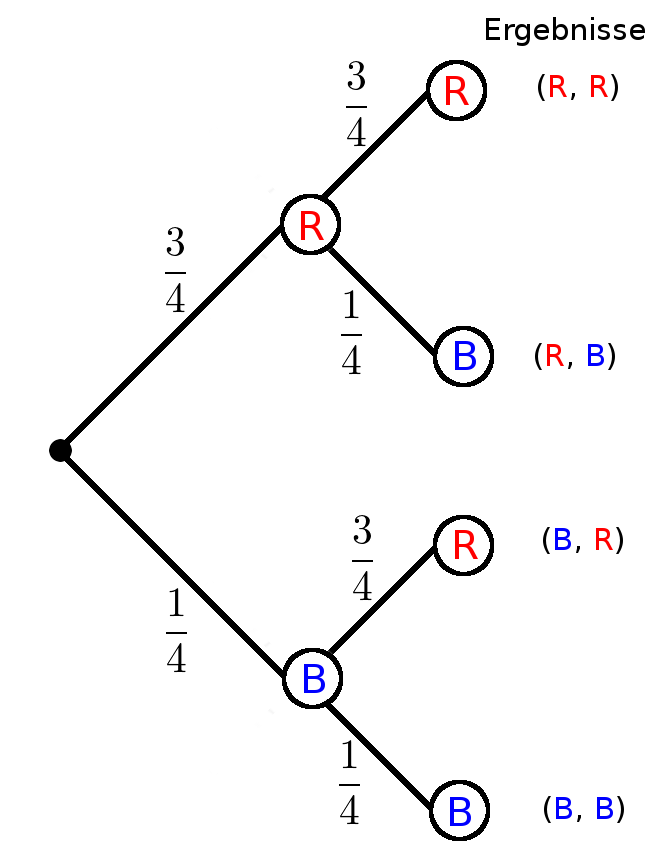
Berechne die Wahrscheinlichkeit für rot und blau unabhängig von der Reihenfolge.

1. Ereignis

   Wiederholung Ergebnismenge und Ereignis
   
   Ergebnismenge:
   $\Omega=\{(R,R);(R,B);$ $(B,R);(B,B)\}$
   
   Ereignis:
   $E:\text{„rot und blau“}$
   $E=\{(R,B);(B,R)\}$

2. Produktregel (1. Pfadregel)

   Wahrscheinlichkeiten der einzelnen Ergebnisse berechnen
   
   $P(R, B)=\frac34\cdot\frac14=\frac{3}{16}$
   $P(B, R)=\frac14\cdot\frac34=\frac{3}{16}$

3. Summenregel (2. Pfadregel)

   Wahrscheinlichkeiten addieren.
   
   $P(E)$ $=P(R, B)+P(B, R)$ $=\frac{3}{16}+\frac{3}{16}$ $=\frac{6}{16}$