Relative position of plane and plane
A distinction is made between three possible relative positions between two planes $E$ and $F$.
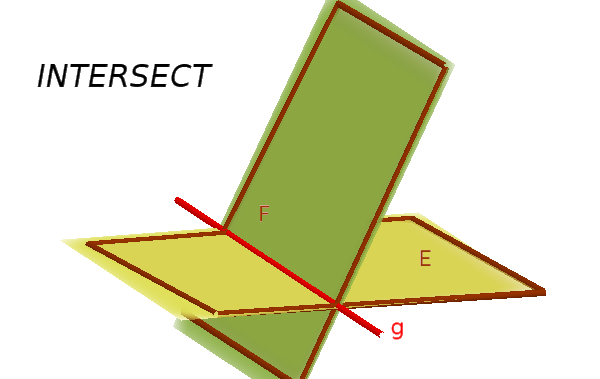
- They intersect.
- They are parallel.

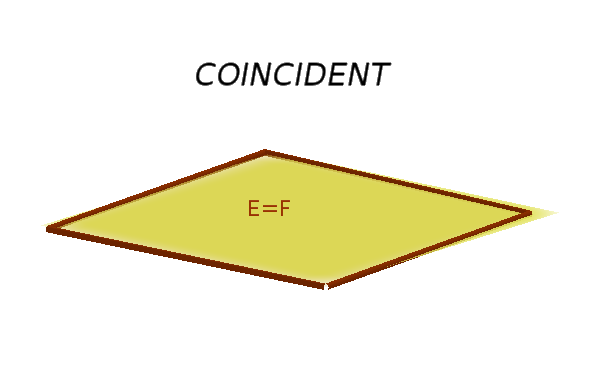
- They are coincident.
Remember
Similar to the relative position of a line and a plane, one tries to calculate the intersection line.
However, if you come across a true statement (e.g. 0 = 0), the planes are coincident. If the statement is incorrect (e.g. 8 = 0), they are parallel.
Hint
Example
$\text{E: } x-y+z=2$
$\text{F: } 2x+y+z=4$
-
Set up a system of equations
The two equations can be viewed as a system of equations.- $x-y+z=2$
- $2x+y+z=4$
Now you should eliminate a variable. This is achieved here, for example, by adding the two equations.
I.+II.
$3x+2z=6$
-
Replace variable with $r$
One of the other variables is now replaced by $r$ and inserted in the equation. For example x:$\color{red}{x=r}$
$3r+2z=6$
The other variable ($z$) can now be expressed as a function of $r$. Simply solve equation for $z$.
$3r+2z=6\quad|-3r$
$2z=6-3r\quad|:2$
$\color{red}{z=3-1.5r}$One of the two plane equations can also be used to determine $y$ by using $x$ and $z$.
$x-y+z=2$
$r-y+(3-1.5r)=2$
$-0.5r-y+3=2\quad|+y$
$-0.5r+3=2+y\quad|-2$
$\color{red}{y=-0.5r+1}$ -
Set up equation of a line
First we write the results for $x$, $y$ and $z$ among themselves.- $x=r$
- $y=-0.5r+1$
- $z=3-1.5r$
Sorted:
- $x=\color{blue}{0}\color{green}{+1}r$
- $y=\color{blue}{1}\color{green}{-0.5}r$
- $z=\color{blue}{3}\color{green}{-1.5}r$
This can now be easily put into the form of a equation of a line.
$\vec{x} = \begin{pmatrix} \, \\ \, \\ \, \end{pmatrix} + r \cdot \begin{pmatrix} \, \\ \, \\ \, \end{pmatrix}$
$\vec{x} = \begin{pmatrix} \color{blue}{0} \\ \color{blue}{1} \\ \color{blue}{3} \end{pmatrix} + r \cdot \begin{pmatrix} \color{green}{1} \\ \color{green}{-0.5} \\ \color{green}{-1.5} \end{pmatrix}$
Example (parallel)
$\text{E: } x-y+z=2$
$\text{F: } 2x-2y+2z=7$
-
Set up a system of equations
- $x-y+z=2\,\,\,|\cdot(-2)$
- $2x-2y+2z=7$
We apply the addition method.
- $-2x+2y-2z=-4$
- $2x-2y+2z=7$
I.+II.
$0=3$ f. s. -
Interpret the result
We obtain a contradiction or a false statement.$0\neq3$
$E$ and $F$ therefore have no common point. The planes must be parallel.
=> $E$ and $F$ are parallel
