Die Exponentialfunktion
Exponentialfunktionen besitzen eine konstante Basis und das $x$ befindet sich im Exponenten. Eine Exponentialfunktion, deren Graph nicht verschoben und nicht gestreckt wurde, besitzt die Funktionsgleichung:
$y=b^x$
Man nennt diese Funktion eine Exponentialfunktion zur Basis $b$. Wichtig ist, dass $b > 0$ und $b\neq1$. Exponentialfunktionen beschreiben exponentielles Wachstum.
i
Eigenschaften
- Der Wertebereich $W=[0,\infty]$ und der Definitionsbereich $D=\mathbb{R}$ (reelle Zahlen)
- Eine Exponentialfunktion, deren Graph nicht veschoben ist, hat keine Nullstellen, denn die x-Achse ist eine Asymptote (Graph nähert sich an, erreicht sie jedoch nie)
- Der Graph verläuft durch die Punkte $P(0|1)$ und $P(1|b)$
- Wenn $b > 1$, ist die Funktion monoton steigend
- Wenn $0 < b < 1$, ist die Funktion monoton fallend
Beispiel
$\color{blue}{f(x)=2^x}$
$\color{red}{g(x)=(\frac12)^x}$
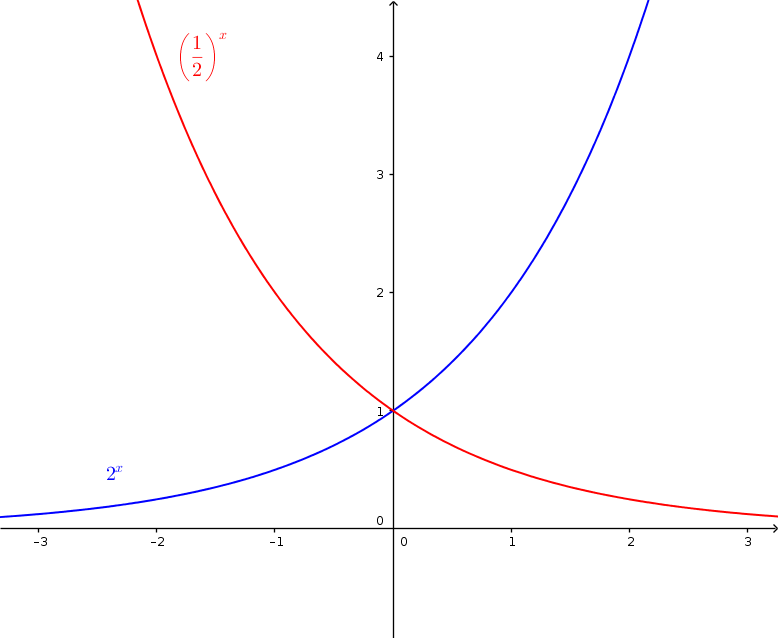
Bei den beiden Graphen der Exponentialfunktionen fallen folgende Eigenschaften auf:
- Beide Funktionen besitzen einen Wertebereich von $W=[0,\infty]$, denn kein y-Wert geht in den Minusbereich.
- Der Definitionsbereich $D=\mathbb{R}$ sind alle reellen Zahlen, denn $x$ kann jede beliebige Zahl sein.
- Die Graphen beider Funktionen nähern sich immer weiter der x-Achse an ($y=0$), erreichen diese jedoch nie. Die x-Achse ist daher eine Asymptote.
- Beide Graphen verlaufen durch die Punkte $P(0|1)$ und $P(1|b)$.
- Die Funktion $\color{blue}{f(x)}$ ist monoton steigend, denn die y-Werte werden mit zunehmenden x-Werten immer größer.
Die Funktion $\color{red}{g(x)}$ ist monoton fallend, denn die y-Werte werden mit zunehmenden x-Werten immer kleiner.
