Verschieben

a) entlang der y-Achse

Der Graph einer Exponentialfunktion wird mit dem Parameter $d$ entlang der y-Achse verschoben. Dabei ändert sich die Asymptote und der Wertebereich. Die allgemeine Formel lautet:

$y=b^x+d$

Merke

Wenn $d > 0$, wird der Graph nach oben verschoben.
Wenn $d < 0$, wird der Graph nach unten verschoben und erhält eine Nullstelle.

Die Asymptote ist bei $y=d$.
Der Wertebereich ist $W=[d,\infty]$

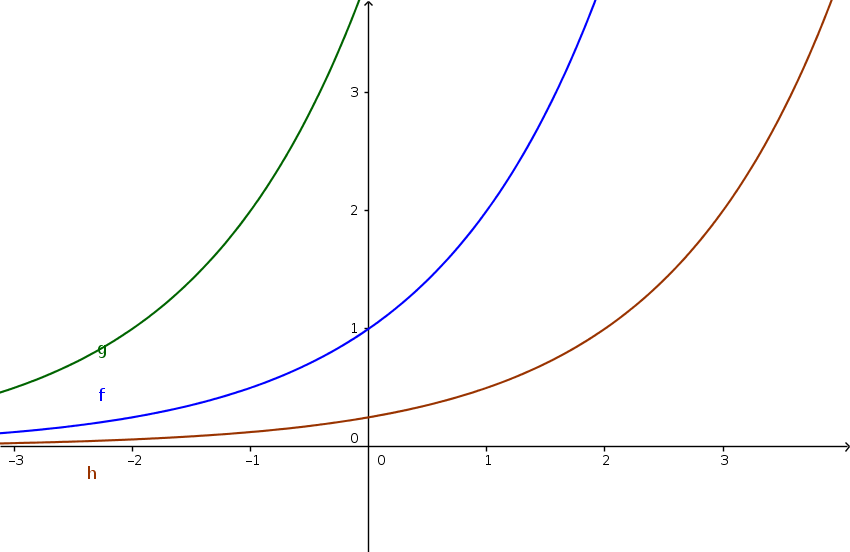
Beispiel

$\color{blue}{f(x)=2^x}$
$\color{green}{g(x)=2^x+2}$
$\color{brown}{h(x)=2^x-2}$

b) entlang der x-Achse

Der Graph einer Exponentialfunktion wird mit dem Parameter $c$ entlang der x-Achse verschoben. Die allgemeine Formel lautet:

$y=b^{x+c}$

Merke

Wenn $c$ > 0, wird der Graph nach links verschoben und entspricht einer Streckung mit $b^c$.
Wenn $c$ < 0, wird der Graph nach rechts verschoben und entspricht einer Stauchung mit $(\frac{1}{b})^c$.

Beispiel

$\color{blue}{f(x)=2^x}$
$\color{green}{g(x)=2^{x+2}}$
$\color{brown}{h(x)=2^{x-2}}$