Math ↠ Exponential functions ↠ Exponential function

The exponential function

Exponential functions have a constant basis and the $x$ is in the exponent. An exponential function whose graph has not been shifted and not stretched has the function equation:

$y=b^x$

This function is called an exponential function to base $b$. It is important that $b > 0$ and $b\neq1$. Exponential functions describe exponential growth.

i

Properties

  • The range of values $W=[0,\infty]$ and the domain $D=\mathbb{R}$ (real numbers)
  • An exponential function whose graph is not shifted has no zeros, because the x-axis is anasymptote (graph approaches, but never reaches)
  • The graph passes through the points $P(0|1)$ and $P(1|b)$
  • If $b > 1$, the function is monotonically increasing
  • If $0 < b < 1$, the function is monotonically decreasing

Example

$\color{blue}{f(x)=2^x}$
$\color{red}{g(x)=(\frac12)^x}$


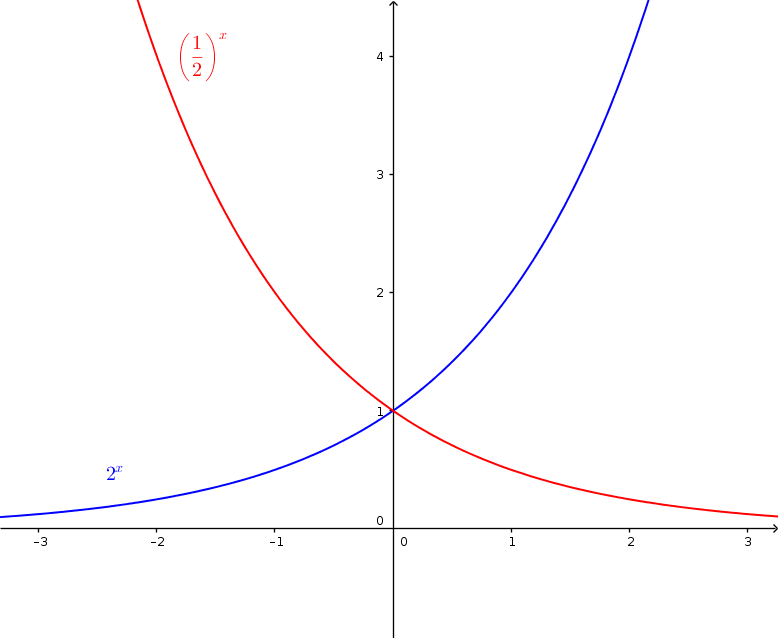
The two graphs of the exponential functions have the following properties:

  1. Both functions have a value range of $W=[0,\infty]$, because no y value goes negative.
  2. The domain $D=\mathbb{R}$ are all real numbers, because $x$ can be any number.
  3. The graphs of both functions continue to approach the x-axis ($y=0$), but never reach it. The x-axis is therefore an asymptote.
  4. Both graphs pass through the points $P(0|1)$ and $P(1|b)$.
  5. The function $\color{blue}{f(x)}$ monotonically increases, because the y values increase with increasing x-values.
    The function $\color{red}{g(x)}$ monotonically decreases, because the y-values get smaller with increasing x-values.