Natural exponential function
The natural exponential function is often referred to as e-function. The name comes from the Euler number $e$, which forms the basis of the exponential function for an e-function. The e-function has the function equation:
$y=e^x$
!
Remember
The Euler number is denoted by $e$ and, like $\pi$ is a constant, irrational number. The Euler number has the value $e = 2,7182818...$.
i
Tip
The derivative of the e-function $f(x)=e^x$ is also $f'(x)=e^x$. The following applies:
$f(x)=f'(x)$
$f(x)=f'(x)$
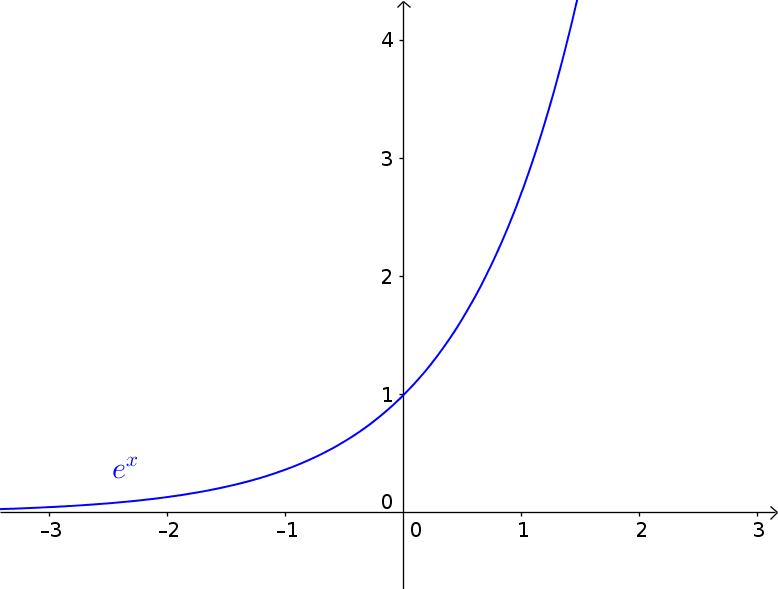
This is the e-function with $f(x)=e^x$:
i
Properties
- The range of values $W=[0,\infty]$ and the domain $D=\mathbb{R}$ (real numbers)
- The e-function has no zeros, because the x-axis is an asymptote (graph approaches, but never reaches)
- The intersection with the y-axis is at $P(0|1)$.
- The graph monotonically increases
