Натуральная показательная функция
Натуральная показательная функция часто упоминается как, e-функция. Название происходит от числа Эйлера $e$,которое образует основу показательной функции для e-функции. Е-функция имеет функциональное уравнение:
$y=e^x$
!
Запомни
Число Эйлера обозначается через $e$ и, как $\pi$ это постоянное,иррациональное число.Число Эйлера имеет значение $e = 2,7182818...$.
i
Совет
Производная от е-функции $f(x)=e^x$ и $f'(x)=e^x$. Применяют следующее:
$f(x)=f'(x)$
$f(x)=f'(x)$
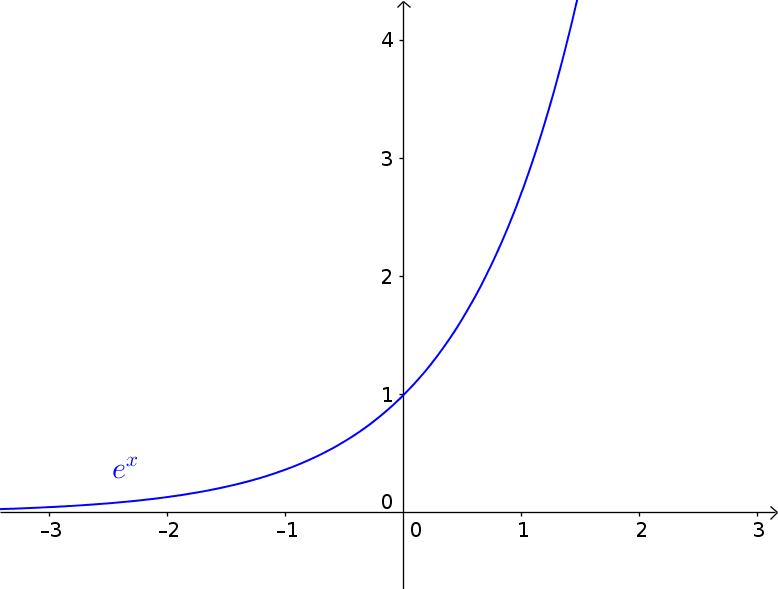
Это е-функция с $f(x)=e^x$:
i
Свойства
- Диапазон значений $W=[0,\infty]$ а домен $D=\mathbb{R}$ (действительные числа)
- E-функция не имеет нулей, потому что ось x является асимптотой (график приближается, но никогда не достает)
- Пересечение с осью y находится в точке $P(0|1)$.
- График монотонно возрастает
