Locus curve
The extrema or inflection points of all function graphs of a family of curves lie on a new graph, the locus curve.
i
Info
In general, locus is a set of points satisfying some condition.
!
Remember
In this case, the locus curve is a new function, on whose graph there is a specific point (e.g. extrema or inflection point) of each function of the family of curves.
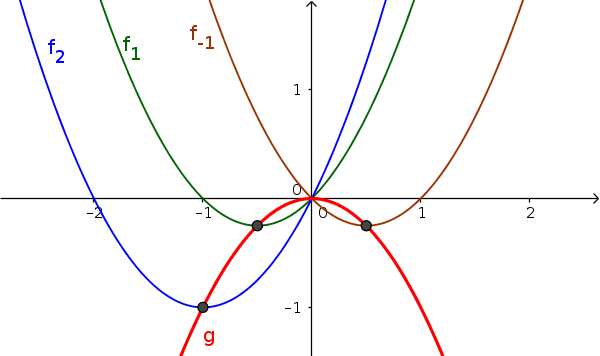
The picture: All minima of the family of curves $f_a$ lie on the graph of a new function $g$.
i
Method
- Calculate searched points (e.g. extrema or inflection points)
- Set up equations for x and y values
- Rearrange equation for x-value and insert
Example
Determine the function of all minima of $f_a(x)=x^2+ax$ ($a\in\mathbb{R}$)
-
Find derivative
$f_a(x)=x^2+ax$
$f_a'(x)=2x+a$
$f_a''(x)=2$ -
Calculate minimum
calculate extrema: Set first derivative equal to zero
$f_a'(x)=0$
$2x+a=0\quad|-a$
$2x=-a\quad|:2$
$x_E=-\frac{a}2$
use suspicious points for extrema in the second derivative test:
$f_a''(-\frac{a}2)=2>0$ => minimum
calculate the y-coordinate and specify the minimum:
$f_a(-\frac{a}2)$ $=(-\frac{a}2)^2+a\cdot(-\frac{a}2)$ $=\frac{a^2}4-\frac{a^2}2$ $=\frac{a^2}4-\frac{2a^2}4$ $=-\frac{a^2}4$
$T(-\frac{a}2|-\frac{a^2}4)$ -
Set up equations for x and y values
from the coordinates of the minimum you can now set up two equations
$T(-\frac{a}2|-\frac{a^2}4)$
$x=-\frac{a}2$
$y=-\frac{a^2}4$ -
Rearrange equation and insert
the equation for x is now changed to the parameter $a$ and inserted into the second one.
$x=-\frac{a}2\quad|\cdot(-2)$
$a=-2x$
$y=-\frac{a^2}4$
$y=-\frac{(-2x)^2}4$ $=-\frac{4x^2}4$ $=-x^2$
function of all minima: $y=-x^2$
