Math ↠ Pythagorean theorem ↠ The right triangle altitude theorem

The right triangle altitude theorem

If you put the altitude on the hypotenuse, it divides a triangle into two individual triangles, which are each right-angled. With the help of the Pythagorean theorem, further properties are derived. That is why it is called the right triangle altitude theorem.

The square of the altitude is the same size as the product of the hypotenuse sections.

i

Method

  1. Find the right angle
  2. Drag the height through the right angle and divide the hypotenuse into 2 sections
  3. Change the formula appropriately, so that the side, you are looking for, is alone
  4. If the height is being searched: Pull the square root ($\sqrt{}$) from the result

Example


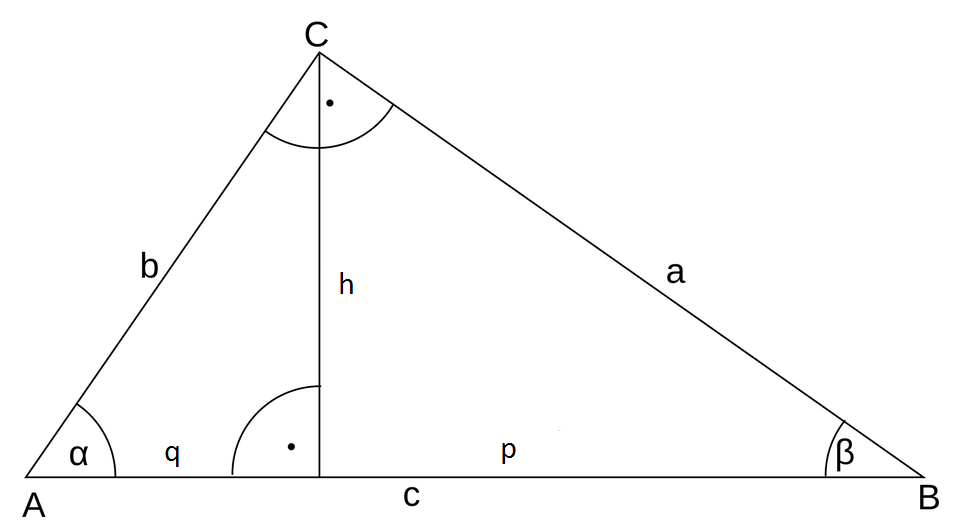
In the triangle ABC with $\gamma=90^\circ$ the right triangle altitude theorem is:

$p\cdot q=h^2$


This is how you calculate the individual sides:

  • $h^2=p\cdot q$ $\Leftrightarrow$ $h=\sqrt{p\cdot q}$

  • $p=\frac{h^2}{q}$

  • $q=\frac{h^2}{p}$