Math ↠ Pythagorean theorem ↠ The Pythagorean theorem

Pythagorean theorem

One side of a right triangle can be calculated with the Pythagorean theorem if the other two sides are known.

The Pythagorean theorem says:

$\text{cathetus}^2 + \text{cathetus}^2$ $= \text{hypotenuse}^2$
i

Method

  1. Find the right angle
  2. Change the formula appropriately, so that the side, you are looking for, is alone
  3. Pull the square root of the result ($\sqrt{}$)

Example


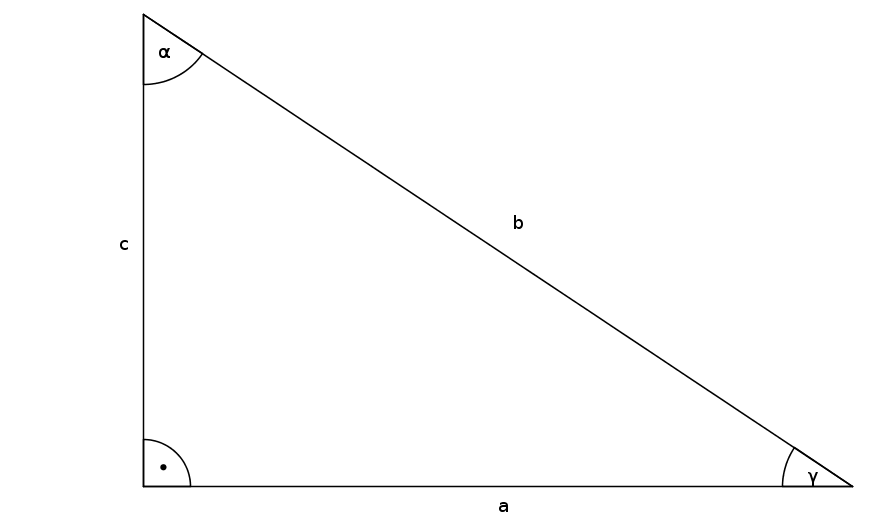
In this triangle ABC with $\beta=90^\circ$, the Pythagorean theorem is:

$a^2+c^2=b^2$

(Because in this case, $a$ and $c$ are the catheti and $b$ is the hypotenuse)

i

Hint

You often get to know the Pythagorean theorem as $a^2+b^2=c^2$ which is not always correct.

Here, the sides were purposely named differently. You have to realize that you always determine the catheti and hypotenuse before.

In our example, the individual sides are calculated as follows:

  • $b^2=a^2+c^2$ $\Leftrightarrow$ $b=\sqrt{a^2+c^2}$

  • $a^2=b^2-c^2$ $\Leftrightarrow$ $a=\sqrt{b^2-c^2}$

  • $c^2=b^2-a^2$ $\Leftrightarrow$ $c=\sqrt{b^2-a^2}$