Altitude-on-hypotenuse theorem
If you put the altitude on the hypotenuse, it divides a triangle into two individual triangles, which are each right-angled. With the help of the Pythagorean theorem, further properties are derived. That is why it is called Altitude-on-hypotenuse theorem.
A square of cathetus of a right triangle is the same size as the rectangle of hypotenuse and the adjacent hypotenuse section.
i
Method
- Find the right angle
- Drag the height through the right angle and divide the hypotenuse into 2 sections
- Change the formula appropriately, so that the side, you are looking for, is alone
- If a cathetus is being searched: Pull the square root ($\sqrt{}$) from the result
Example
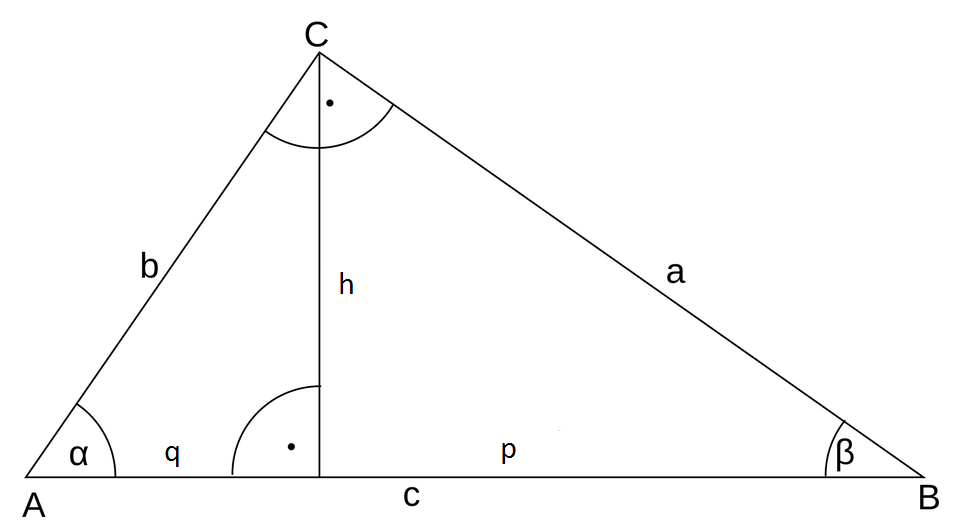
In the triangle ABC with $\gamma=90^\circ$ the altitude-on-hypotenuse theorem is:
$p\cdot c=a^2$
- $a^2=p\cdot c$ $\Leftrightarrow$ $a=\sqrt{p\cdot c}$
- $p=\frac{a^2}{c}$
- $c=\frac{a^2}{p}$
$q\cdot c=b^2$
- $b^2=q\cdot c$ $\Leftrightarrow$ $b=\sqrt{q\cdot c}$
- $q=\frac{b^2}{c}$
- $c=\frac{b^2}{q}$
