Natural exponential function
A special kind of exponential function is the natural exponential function or exponential function with base e.
$f(x)=e^x$
Derivation
The derivative of an exponential function, however, is precisely itself shifted to the right or left.
Example: $f(x)=2^x$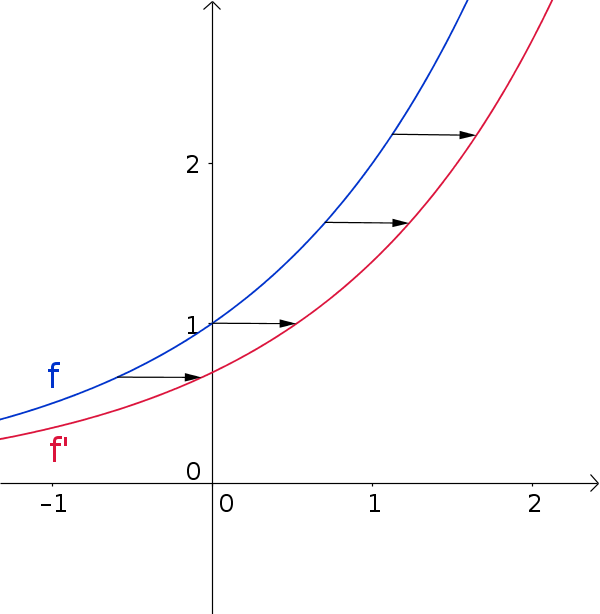
Now one can try to make the distance of the shifted derivative ever smaller. So there must be exactly one derivative whose distance is zero and therefore matches the function.
Leonhard Euler (1707-1783) found just this exponential function, which does not shift when derived and thus gives the initial function.
$f(x)=e^x=f'(x)$
!
Remember
The natural exponential function is a exponential function with Euler's number as a base.
Derived again results in the identical function:
$f(x)=e^x$
$f'(x)=e^x$
Derived again results in the identical function:
$f(x)=e^x$
$f'(x)=e^x$
i
Hint
The Euler number $e$ like $\pi$, is a constant, irrational number. It is $e = 2,7182818...$.
