Natürliche Exponentialfunktion
Eine spezielle Art der Exponentialfunktion ist die natürliche Exponentialfunktion oder auch e-Funktion:
$f(x)=e^x$
Herleitung
Die Ableitung einer Exponentialfunktion ist ebendiese jedoch nach rechts oder links verschoben.
Beispiel: $f(x)=2^x$
Nun kann man versuchen, den Abstand der verschobenen Ableitung immer kleiner werden zu lassen. Es muss also genau eine Ableitung geben, deren Abstand null ist und die daher mit der Funktion übereinstimmt.
Leonhard Euler (1707-1783) fand ebendiese Exponentialfunktion, welche sich abgeleitet nicht verschiebt und somit wieder die Ausgangsfunktion ergibt.
$f(x)=e^x=f'(x)$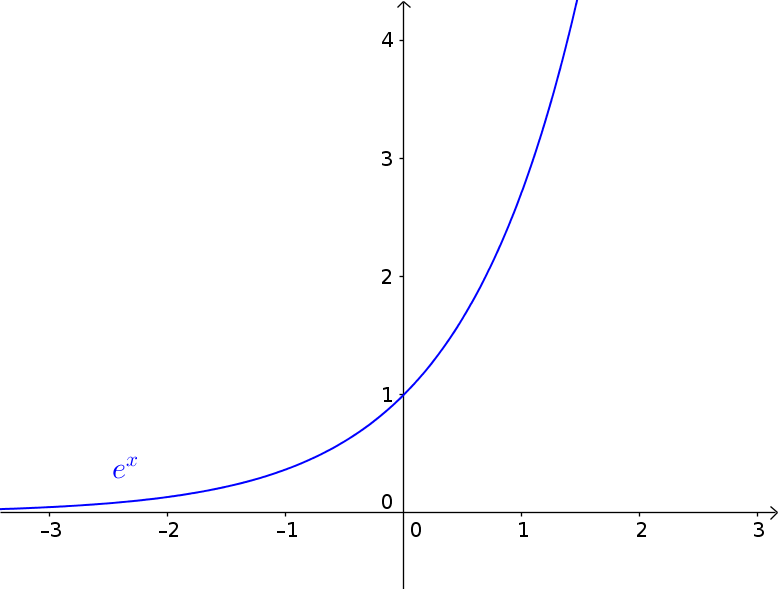
!
Merke
Die e-Funktion ist eine Exponentialfunktion mit der eulerschen Zahl als Basis.
Abgeleitet ergibt sich wieder die identische Funktion:
$f(x)=e^x$
$f'(x)=e^x$
Abgeleitet ergibt sich wieder die identische Funktion:
$f(x)=e^x$
$f'(x)=e^x$
i
Tipp
Die eulersche Zahl $e$ ist ähnlich wie $\pi$ eine konstante, irrationale Zahl. Es gilt $e = 2,7182818...$.
