Derivatives of exponential functions
When computing the derivative of general exponential functions one uses the natural logarithm.
!
Remember
$f(x)=a^x$
$f'(x)=a^x\cdot\ln(a)$
$f'(x)=a^x\cdot\ln(a)$
Example
$f(x)=2^x$
$f'(x)=2^x\cdot\ln(2)$
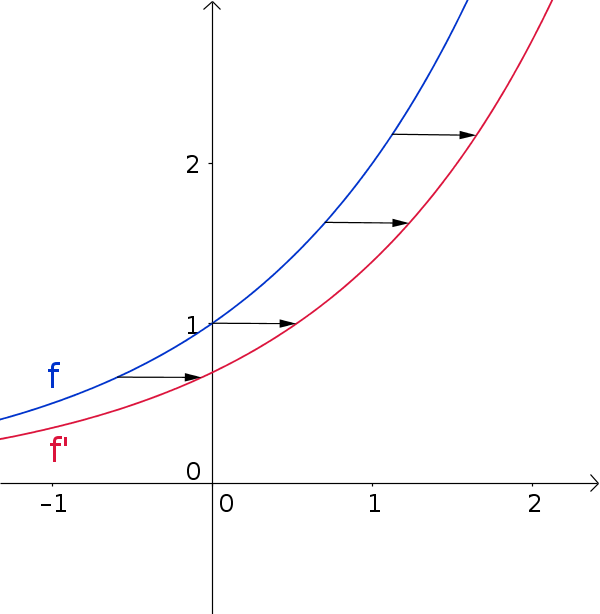
When computing the derivative of an exponential function, it shifts along the x-axis.
Derivation
Here the derivation of the phrase is described.
We are looking for the derivative of $f(x)=a^x$
Rewrite as exponential function
Since the ln-functionis the inverse of the exponential function, the following applies:
$x=e^{\ln(x)}$
$a^x=e^{\ln(a^x)}$Now the logarithm law for powers is applied.
$f(x)=a^x=e^{x\cdot\ln(a)}$
$a^x=e^{x\cdot\ln(a)}$Compute the derivative of the exponential function
$f(x)=e^{g(x)}$
$f'(x)=e^{g(x)}\cdot g'(x)$
$f(x)=e^{x\cdot\ln(a)}$
$f'(x)=e^{x\cdot\ln(a)}\cdot(x\cdot\ln(a))'$$\ln(a)$is a constant factor (constant factor rule) and $(x)'=1$
$f'(x)=e^{x\cdot\ln(a)}\cdot\ln(a)$Rewrite exponential function
Apply the method from the first step backwards:
$a^x=e^{x\cdot\ln(a)}$
$f'(x)=e^{x\cdot\ln(a)}\cdot\ln(a)$
$f'(x)=a^x\cdot\ln(a)$
