Das Federpendel
Bei dem Federpendel wird die rücktreibende Kraft durch eine Feder beigesteuert.
Hierbei geht man von einer idealen Feder aus, die immer eine zur Auslenkung proportionale Kraft auswirkt.
i
Info
Reale Federn haben ab einer bestimmten Auslenkung keine proportionale Abhängigkeit mehr zu ihrer Kraft.
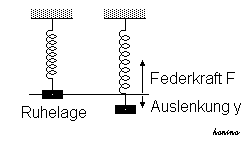
The original uploader was Honina at German Wikipedia. [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0/)]
Die Schwingungskonstante des harmonischen Oszillators D ist in diesem Fall die Federkonstante, die ebenfalls das Formelzeichen $D$ hat.
Die Schwingungsgleichung eines Federpendels ist also:
$s(t) = A\cdot \sin(\sqrt{\frac{D}{m}}\cdot t+\varphi )$
Wenn mehere Federn zusamengeschaltet werden gilt für die resultierende Federkonstante $D_{ges}$:
- Parallelschaltung: $D_{ges}=D_1+D_2+...$
- Reihenschaltung: $\frac{1}{D_{ges}} = \frac{1}{D_1}+ \frac{1}{D_2}+...$
