Waagerechter Wurf

Eine Wurfbewegung kann natürlich auch waagerecht ablaufen.

Den Verlauf des Fluges können wir in einem Diagramm darstellen. Dabei dient sowohl die X-, als auch die Y-Achse als Maßstab für die Strecke.
Wir können nun unabhängig die Fallzeit berechnen und anschließend die Flugweite. Zuletzt ermitteln wir die Aufprallgeschwindigkeit und den Winkel.

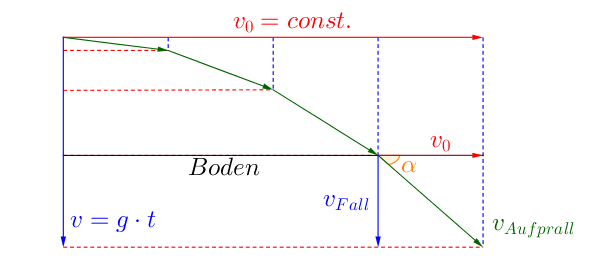
Um eine solche Bewegung grafisch darzustellen, werden die einzelnen Bewegungen entlang der Achsen gezeichnet. Im Anschluss werden gleiche Zeitpunkte mit Geraden verbunden und eine neue Kurve gezeichnet (grün).

Beispiel

Ein Fahrradfahrer fährt mit 10m/s über eine 1m hohe waagerechte Schanze. Berechne wie lange er in der Luft ist, wie weit er fliegt, und mit welcher Geschwindigkeit er aufkommt.

Formeln:

Fortbewegung: $s=10\frac{m}s\cdot t$
Fallbewegung: $s=\frac{-g}{2}\cdot t^2+1m$

1. Flugzeit

   Zunächst bestimmen wir die Flugzeit, indem wir berechnen, wann der Boden erreicht wird.
   
   $0m=\frac{-g}{2}\cdot t^2+1m$
   
   $\frac{g}2\cdot t^2=1m$
   
   $t^2=\frac{2m}{g}$
   
   $t^2=0,2s^2$
   $t=0,45s$

2. Flugstrecke

   Nun können wir bestimmen, wie weit der Fahrradfahrer springt.
   
   $s=10\frac{m}s\cdot0,45s=4,5m$

3. Aufprallwinkel und -geschwindigkeit

   Erst brauchen wir die Teilgeschwindigkeiten zum Zeitpunkt des Aufpralls.
   
   $v_\text{Fortbewegung}=10\frac{m}{s}$
   $v_\text{Fall}=g\cdot0,45s=4,4\frac{m}s$
   
   Die Aufprallgeschwindigkeit ist nun:
   
   $v_\text{Aufprall}^2=100\frac{m^2}{s^2}+19,36\frac{m^2}{s^2}$ $=119,36\frac{m^2}{s^2}$
   
   $v_\text{Aufprall}\approx10,93\frac{m}s$
   
   Zuletzt lässt sich der Aufprallwinkel mit dem Arkustangens bestimmen.
   
   $\tan{\alpha}=\frac{4,4\frac{m}s}{10\frac{m}s}$
   
   $\alpha=\arctan(\frac{4,4\frac{m}s}{10\frac{m}s})$ $\approx23,7°$