Zeit–Weg–Diagramme
Auch bei gleichmäßig beschleunigten Bewegungen kann man die zurückgelegte Strecke s in Relation zur vergangenen Zeit t setzen. Dies geschieht im Zeit–Weg–Diagramm oder in einer Zeit–Weg–Tabelle.
Allerdings ist es hierbei etwas schwerer als bei einer gleichförmigen Bewegung. Das folgende Beispiel zeigt das Problem:
Beschleunigung: $1\frac{m}{s^2}$
| Zeit $t$ in s | Geschwindigkeit $v$ in m/s | Strecke $s$ in m |
|---|---|---|
| 1 | 1 | 0,5 |
| 2 | 2 | 2 |
| 3 | 3 | 4,5 |
| 4 | 4 | 8 |
| 5 | 5 | 12,5 |
| 6 | 6 | 18 |
!
Merke
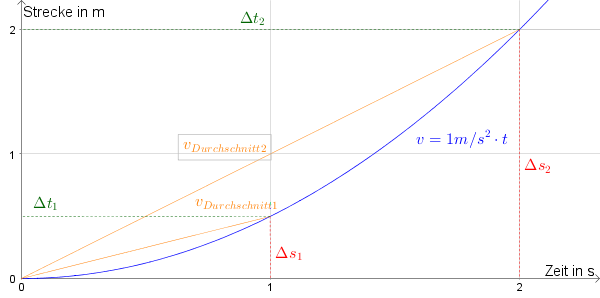
Die zurückgelegte Strecke nimmt nicht gleichmäßig zu, da die Geschwindigkeit nicht konstant ist.
Die allgemeine Funktionsgleichung für die Strecke bei beschleunigten Bewegungen lautet:
$s(t)=\frac12\cdot a\cdot t^2+v_0\cdot t+s_0$
i
Info
Wie man an der Funktion bereits erkennen kann, handelt es sich um eine Funktion 2. Grades, also eine Parabel. Wenn man nun eine Funktion mit der passenden Beschleunigung aufstellt, so wird diese parabelförmig verlaufen.
