Zeit–Geschwindigkeit–Diagramme
Interessant bei beschleunigten Bewegungen ist das Verhalten der Geschwindigkeit. Da diese sich ändert, können aus dem Diagramm alle Werte von Strecke bis Beschleunigung abgelesen werden.
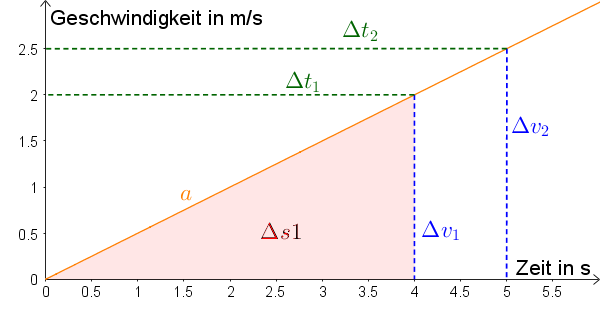
In einem Zeit–Geschwindigkeit–Diagramm entspricht die Steigung der Beschleunigung a. Die Fläche unterhalb der Funktion entspricht der Strecke s. Sie ist daher:
$s(t)=\frac12\cdot a\cdot t^2+v_0\cdot t+s_0$
!
Merke
Die Geschwindigkeit v leitet sich über die Zeit mal die Beschleunigung her, also gilt:
$v(t)=a\cdot t+v_0$
$v(t)=a\cdot t+v_0$
i
Tipp
Wenn man die Funktion s(t) ableitet, erhält man:
$s'(t)=a\cdot t+v_0$
$s'(t)=v(t)$
Daher ist die Ableitung der Strecke die Geschwindigkeit, denn die Steigung im Zeit-Weg-Diagramm entspricht auch der Geschwindigkeit.
$s'(t)=a\cdot t+v_0$
$s'(t)=v(t)$
Daher ist die Ableitung der Strecke die Geschwindigkeit, denn die Steigung im Zeit-Weg-Diagramm entspricht auch der Geschwindigkeit.
