Lineares und proportionales Wachstum
Lineares Wachstum
Bei linearem Wachstum wird der Wert $N(t)$ bei gleicher Zeitspanne ($c$) immer mit dem gleichen Summanden ($d$) addiert.
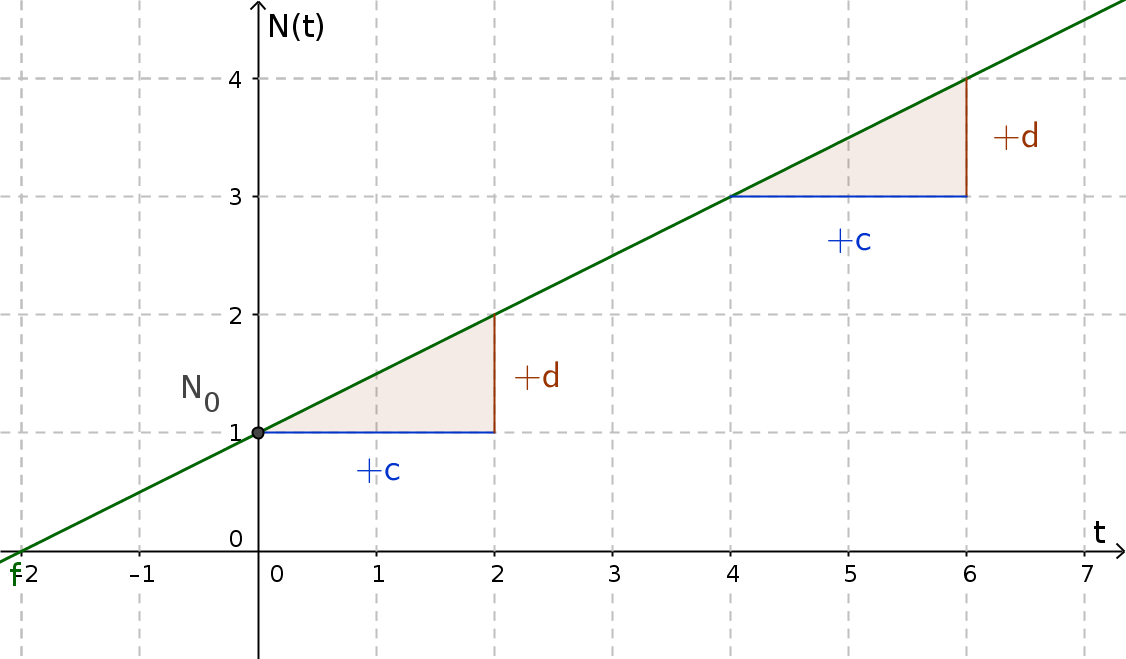
Die allgemeine Gleichung von linearem Wachstum ist:
$N(t)=m\cdot t + N_{0}$
$t...$ Zeitspanne
$m ...$ Wachstumsfaktor
$N(t) ...$ Wert in der Abhängigkeit von $t$
$N_{0} ...$ Anfangsbestand/Startwert
Proportionales Wachstum
Proportionales Wachstum ist wie lineares Wachstum, jedoch mit einem Anfangsbestand von 0.
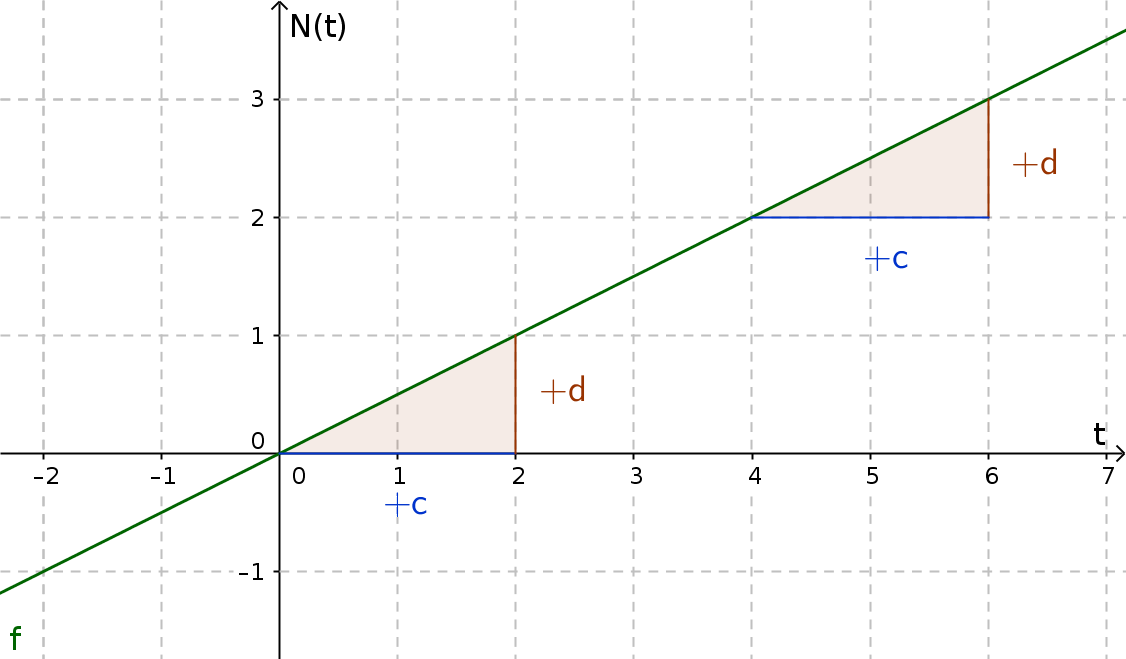
Die allgemeine Gleichung wäre also:
$N(t)=m\cdot t$
$N_{0}$ fällt weg, denn der Startwert beträgt 0.
