Mathe ↠ Wachstumsprozesse ↠ Beschränktes Wachstum

Beschränktes Wachstum

Beschränktes Wachstum wird durch eine natürliche Schranke begrenzt. Das heißt es gibt eine Grenze (Schranke), die das Wachstum nach oben oder unten einschränkt. Der Zuwachs ist abhängig von der Differenz zwischen der Grenze $S$ und der aktuellen Größe. Je größer der Abstand zwischen der Schranke und der Größe ist, desto größer ist auch der Wachstumsfaktor.




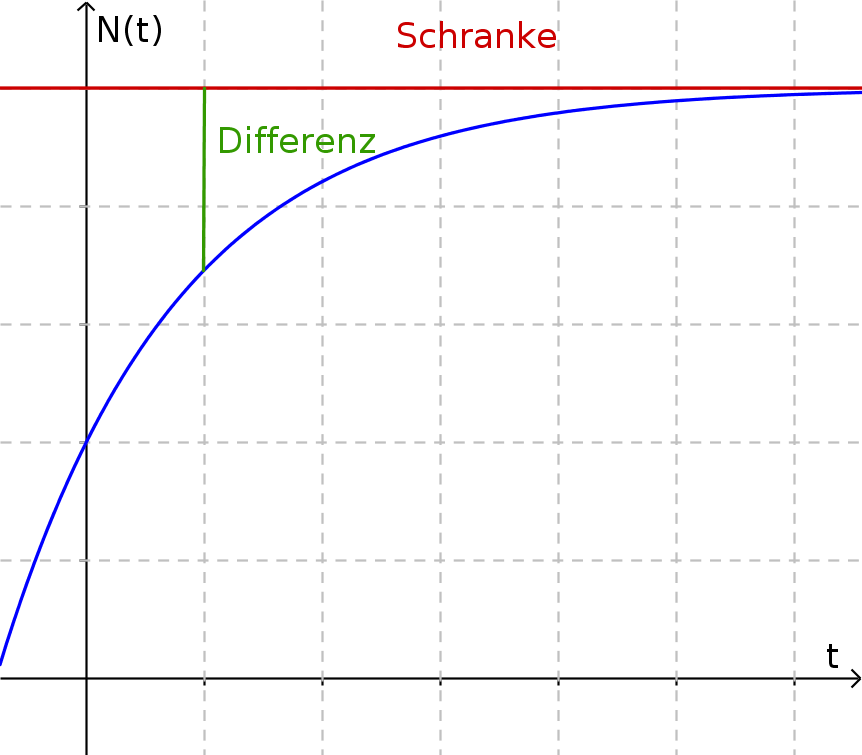
Es ergibt sich folgende rekursive Formel:

$N(t+1)=N(t)+k\cdot(S-N(t))$

$t...$ Zeitspanne
$k ...$ Anteil von der Differenz
$S ...$ Schranke
$N(t) ...$ momentane Größe
$N(t+1) ...$ nachfolgende Größe

!

Merke

Mit einer rekursiven Gleichung lässt sich der Folgewert $N(t+1)$ mit dem vorangegangenen Wert $N(t)$ berechnen.

Beispiel

Eine Tasse mit 85°C warmem Tee wird zum Kühlen bei einer Zimmertemperatur von 22°C abgestellt. Pro Minute kühlt der Tee um 15% der Differenz ab. Wie verhält sich die Temperatur in den nächsten 15 Minuten?

  1. Schranke $S$ und Anteil $k$ einsetzen


    $S=22$
    $k=15\%=0,15$

    $N(t+1)=N(t)+0,15\cdot(22-N(t))$

  2. Wertetabelle anlegen


    $N(0)=85$
    $N(1)=85+0,15\cdot(22-85)$ $=75,55$
    $N(2)=75,55+0,15\cdot(22-75,55)$ $=67,52$
    ...
    $N(15)=27,5$

  3. Funktion einzeichnen



    Nach 15 Minuten hat der Tee eine Temperatur von ca. 27,5°C.
    Es liegt beschränkte Abnahme vor. Der Tee kommt den 22°C immer näher, wird diese jedoch nie erreichen. 22°C ist also die untere Schranke.