Math ↠ Growth and decay ↠ Limited growth

Limited growth

Limited growth is limited by a natural barrier. That is, there is a limit (barrier) that limits growth up or down. The increment depends on the difference between the boundary $S$ and the current size. The larger the distance between the barrier and the size, the larger the growth factor.




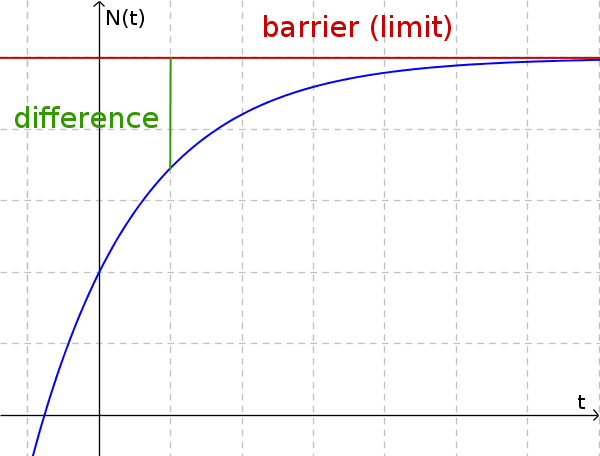
The result is the following recursive formula:

$N(t+1)=N(t)+k\cdot(S-N(t))$

$t...$ period of time
$k ...$ proportion of the difference
$S ...$ barrier
$N(t) ...$ current size
$N(t+1) ...$ subsequent size

!

Remember

With a recursive equation, the following value $N(t+1)$ can be calculated with the previous value $N(t)$.

Example

A cup of 85 ° C tea is served for cooling at a room temperature of 22 ° C. The tea cools by 15% of the difference per minute. How does the temperature behave in the next 15 minutes?

  1. Insert barrier $S$ and proportion $k$


    $S=22$
    $k=15\%=0.15$

    $N(t+1)=N(t)+0.15\cdot(22-N(t))$

  2. Create a value table


    $N(0)=85$
    $N(1)=85+0.15\cdot(22-85)$ $=75.55$
    $N(2)=75.55+0.15\cdot(22-75.55)$ $=67.52$
    ...
    $N(15)=27.5$

  3. Draw in the function



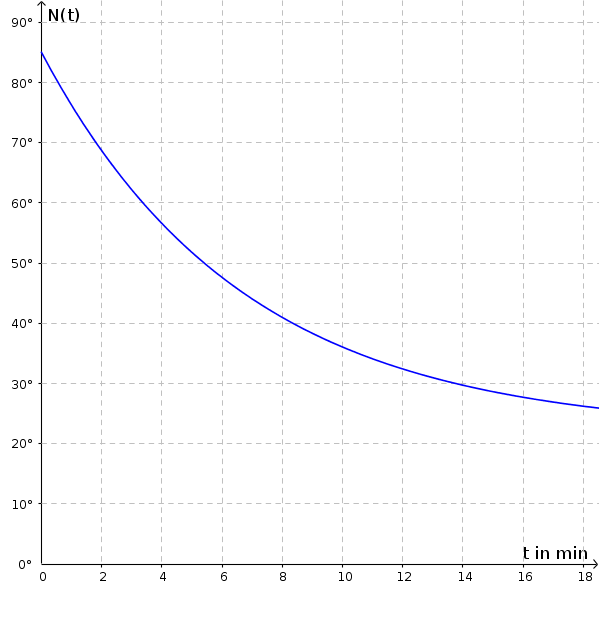
    After 15 minutes, the tea has a temperature of about 27.5 ° C.
    There is limited decrease. The tea gets closer and closer to the 22 ° C, but will never reach it. 22 ° C is the lower bound.