Math ↠ Growth and decay ↠ Exponential increase and decrease

Exponential increase and decrease

Exponential growth denotes both the exponential increase and decrease.

The formula applies:

$N(t)=N_{0}\cdot a^t$
!

Remember

Increase or decrease can be differentiated by the growth factor $a$:
  • If $a>1$, there is an exponential increase.
  • If $0<a<1$, there is anexponential decrease.

Exponential increase

With an exponential increase, the growth factor is always greater than 1. So you get more than you had before.

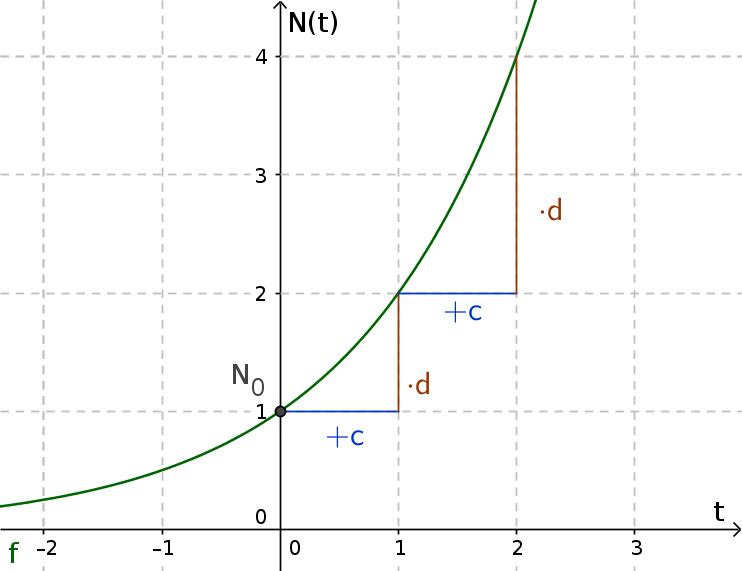
Examples

  • $N(t)=2\cdot3^t$
  • $N(t)=50\cdot(\frac54)^t$

Exponential decrease

At exponential decay, the growth factor is always less than 1 (and greater than 0). The stock thus decreases with increasing $t$.

Since we have a fraction, e.g $\frac1d$ as a growth factor, we can think of this as a division.

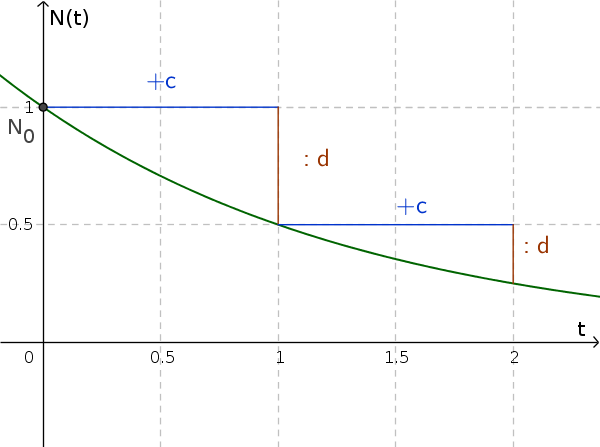
Examples

  • $N(t)=10\cdot(\frac13)^t$
  • $N(t)=\frac12\cdot(\frac78)^t$
  • $N(t)=3\cdot(0.25)^t$
i

Hint

Note that the rule only applies to positive $t$. On the other hand, negative exponents can be rewritten:

$N(t)=N_0\cdot b^{-t}$ $=N_0\cdot (\frac1b)^t$

In this case, we apply the rule above for $a=\frac1b$.

Examples

  • $N(t)=2^{-t}=(\frac12)^t$ ⇒exponential decrease

  • $N(t)=(\frac13)^{-t}=3^t$ ⇒exponential increase