Экспоненциальный рост и спад
Экспоненциальный рост означает как экспоненциальное увеличение, так и экспоненциальный спад.
Применяется формула:
$N(t)=N_{0}\cdot a^t$
!
Запомни
Увеличение или падение могут дифференцироваться фактором роста $a$:
- Если $a>1$, экспоненциальный рост.
- Если $0<a<1$, экспоненциальный спад.
Экспоненциальный рост
При экспоненциальном росте, фактор роста всегда больше 1. Таким образом вы получаете больше, чем у вас было.
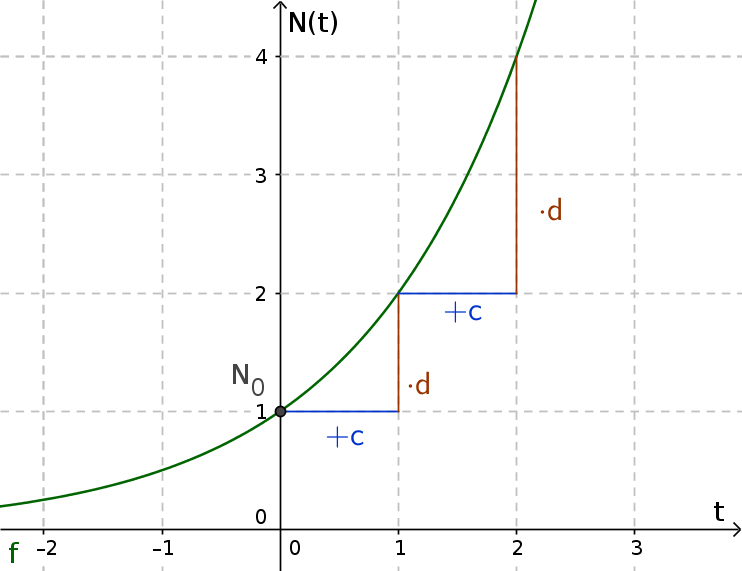
Примеры
- $N(t)=2\cdot3^t$
- $N(t)=50\cdot(\frac54)^t$
Экспоненциальный спад
При экспоненциальном спаде, фактор роста всегда меньше 1 (и больше 0). Линия роста таким образом падает по мере возрастания $t$.
Имея дробь, например $\frac1d$ в качестве фактора роста, мы можем рассматривать ее как деление.
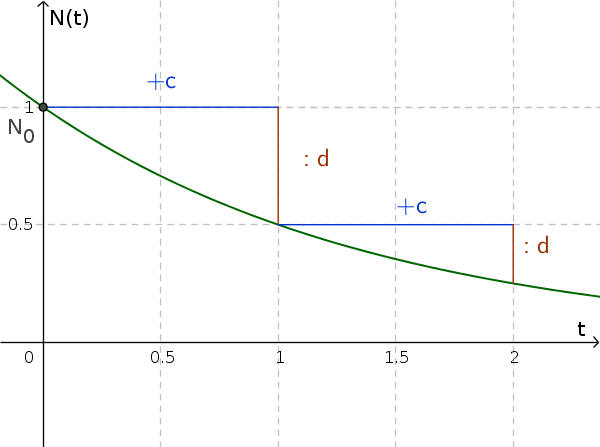
Примеры
- $N(t)=10\cdot(\frac13)^t$
- $N(t)=\frac12\cdot(\frac78)^t$
- $N(t)=3\cdot(0.25)^t$
i
Подсказка
Заметьте, что правило применяется только к положительным $t$. С другой стороны, отрицательные показатели можно переписать:
$N(t)=N_0\cdot b^{-t}$ $=N_0\cdot (\frac1b)^t$
В этом случае, мы применяем правило сверху для $a=\frac1b$.Примеры
- $N(t)=2^{-t}=(\frac12)^t$ ⇒экспоненциальный спад
- $N(t)=(\frac13)^{-t}=3^t$ ⇒ экспоненциальный рост
