Zusammenfassung
Ebenengleichungen
Eine Auflistung verschiedener Ebenengleichungen:
| Parametergleichung | ||
| $\text{E: } \vec{x} = \vec{a} + r \cdot \vec{u} + s \cdot \vec{v}$ | ||
| Normalengleichung | ||
| $\text{E: } (\vec{x} - \vec{a}) \cdot \vec{n}=0$ | ||
| Koordinatengleichung | ||
| $\text{E: } ax+by+cz=d$ | ||
| $\text{E: } \frac{x}a+\frac{y}b+\frac{z}c=1$ | ||
Bei der letzten handelt es sich um die Achsenabschnittsgleichung, eine Spezialform der Koordinatengleichung.
Ebenengleichungen umformen
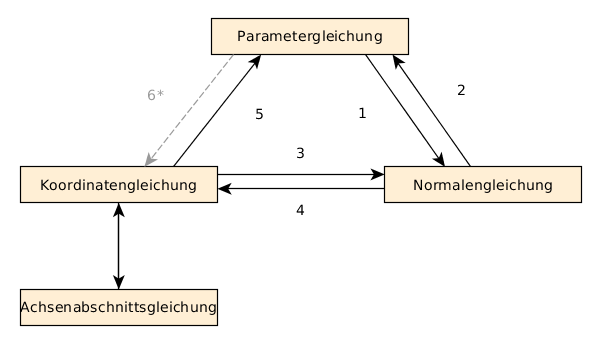
Parametergleichung → Normalengleichung
Normalenvektor berechnen (Skalarprodukt oder Kreuzprodukt) und mit Stützvektor einsetzenNormalengleichung → Parametergleichung
2 Richtungsvektoren finden (senkrecht zum Normalenvektor) und mit Stützvektor einsetzenKoordinatengleichung → Normalengleichung
Normalenvektor ablesen und beliebigen Stützpunkt in der Ebene suchenNormalengleichung → Koordinatengleichung
Ausmultiplizieren (mithilfe des Skalarproduktes)Koordinatengleichung → Parametergleichung
3 beliebige Punkte der Ebene suchen und Parametergleichung aufstellenParametergleichung → Koordinatengleichung
Der Weg ist schwieriger und man sollte stattdessen über die Normalengleichung gehen (erst 1, dann 4).
