Polynomial long division
Cubic equations are 3rd degree polynomial equations and have the form:
In order to solve cubic equations and equations of higher degree one needs the Polynomial long division.
First, a zero is guessed by trial and error and then, using polynomial long division, one can transform the equation into a quadratic equation.
Method
- Guess a zero $x_N$
- Polynomial long division: Divide equation by $(x-x_N)$
- Solve the quadratic equation
Hint
Example
Solve cubic equation: $x^3-19x-30=0$
-
Guess a zero
The first zero must be found by trial and error.
Use different values for $x$ until 0 results.
$x^3-19x-30=0$
$x=1$:
$1^3-19\cdot1-30=-48$ $\neq0$ =>no zero
$x=-1$:
$(-1)^3-19\cdot(-1)-30=-12$ $\neq0$ =>no zero
$x=-2$:
$(-2)^3-19\cdot(-2)-30=-0$ =>zero at $x_{1}=-2$ -
Polynomial long division
The function is divided by $(x-x_1)$. Use polynomial long division for this.
$(x^3-19x-30):(x+2)$First calculate $x^3:x$ and write down the result.

Now $x^2$ is multiplied by $(x+2)$. The result is written in the second line and receives a minus.

Both lines are now added together with the remainder written underneath.
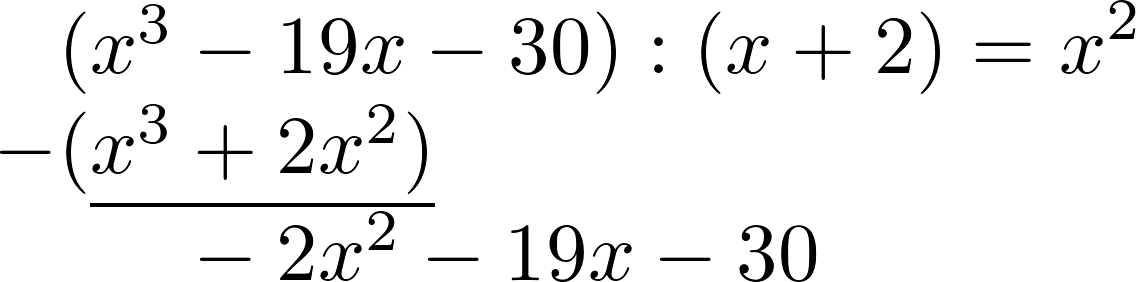
Similarly as before, one now calculates $-2x^2:x$. Write the result to the right and multiply it by $(x+2)$ to put it in the line below.
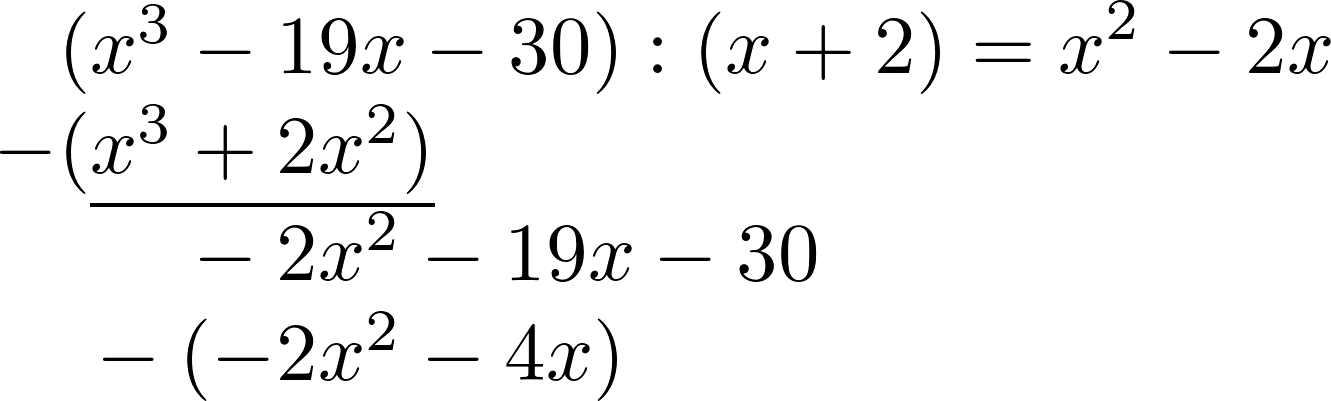
The two lines are subtracted again.
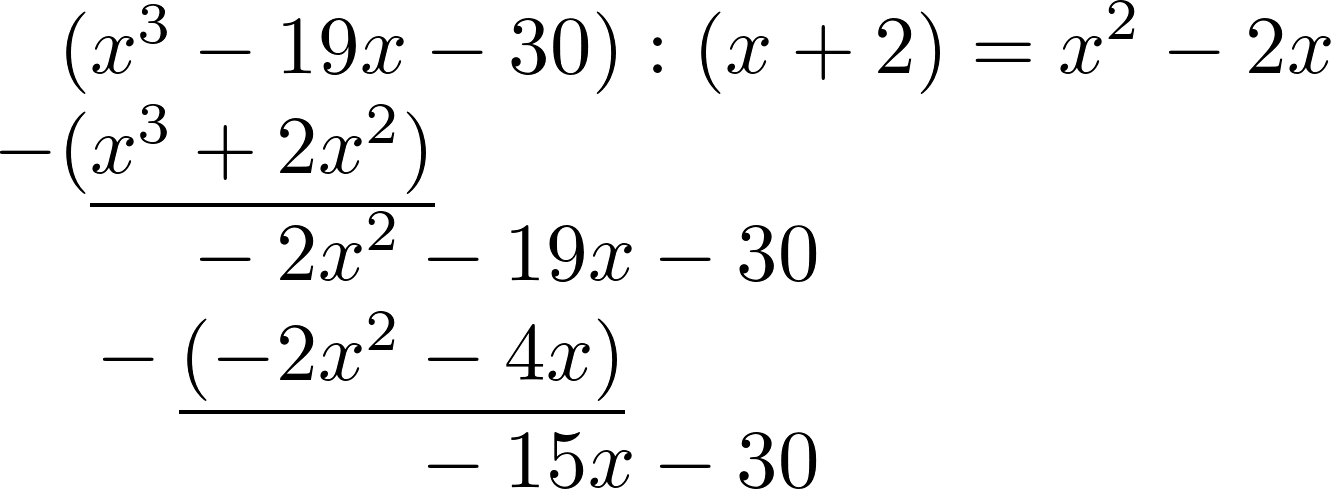
Finally, $-15x:x$ is calculated, multiplied back and deducted. The rest is 0 and the polynomial division is done.
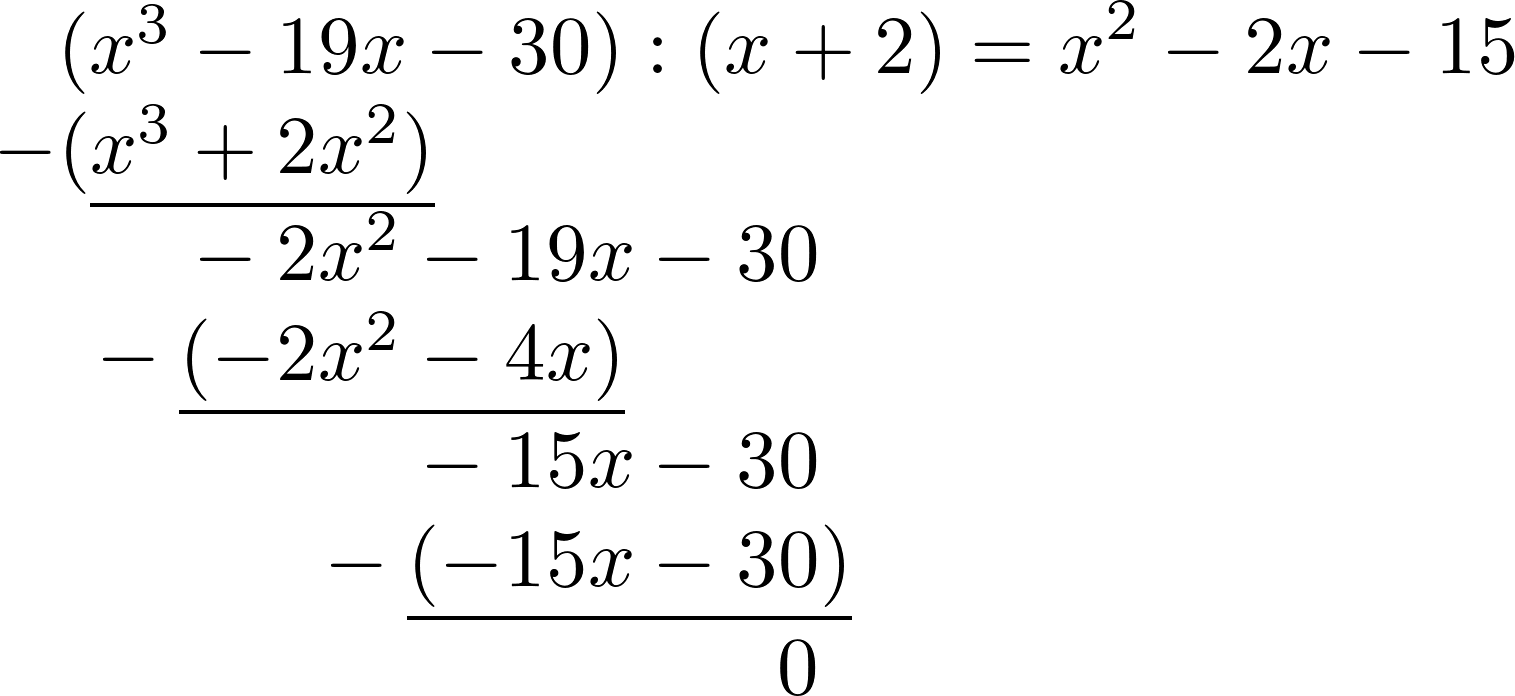
-
Solve quadratic equation
The new quadratic equation can now be solved e. g. with the pq-formula.
$x^2-2x-15=0$
$x_{2,3} = \frac{p}{2} \pm\sqrt{(\frac{p}{2})^2-q}$
$x_{2,3} = 1 \pm\sqrt{1^2+15}$
$x_{2,3} = 1 \pm\sqrt{16}$
$x_{2,3} = 1 \pm4$
$x_2=5$ and $x_3=-3$
The solutions of the initial equation are $x_1=-2$, $x_2=5$ and $x_3=-3$
