Shifting
a) along the y-axis
The graphs of $y=\sin(x)$ and $y=\cos(x)$ are shifted with the value $d$ along the y-axis. The general formula is:
$y=\sin(x)+d$
$y=\cos(x)+d$
$y=\cos(x)+d$
!
Remember
- If $d$ > 0, the graph is shifted up.
- If $d$ < 0, the graph is shifted down.
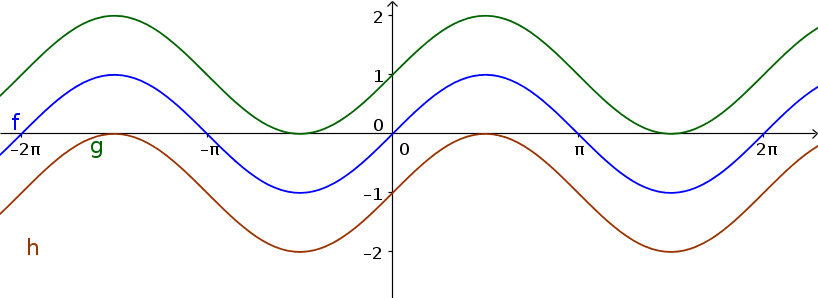
Example
$\color{green}{g(x)=\sin(x)+1}$
$\color{blue}{f(x)=\sin(x)}$
$\color{brown}{h(x)=\sin(x)-1}$
b) along the x-axis
The graphs of $y=\sin(x)$ and $y=\cos(x)$ are shifted with the value $c$ along the x-axis. The general formula is:
$y=\sin(x+c)$
$y=\cos(x+c)$
$y=\cos(x+c)$
!
Remember
- If $c$ > 0, the graph is shifted to the left.
- If $c$ < 0, the graph is shifted to the right.
Example
$\color{green}{g(x)=\sin(x+\frac{\pi}{2})}$
$\color{blue}{f(x)=\sin(x)}$
$\color{brown}{h(x)=\sin(x-\frac{\pi}{2})}$

