Math ↠ Pythagorean theorem ↠ Altitude-on-hypotenuse theorem

Altitude-on-hypotenuse theorem

If you put the altitude on the hypotenuse, it divides a triangle into two individual triangles, which are each right-angled. With the help of the Pythagorean theorem, further properties are derived. That is why it is called Altitude-on-hypotenuse theorem.

A square of cathetus of a right triangle is the same size as the rectangle of hypotenuse and the adjacent hypotenuse section.

i

Method

  1. Find the right angle
  2. Drag the height through the right angle and divide the hypotenuse into 2 sections
  3. Change the formula appropriately, so that the side, you are looking for, is alone
  4. If a cathetus is being searched: Pull the square root ($\sqrt{}$) from the result

Example


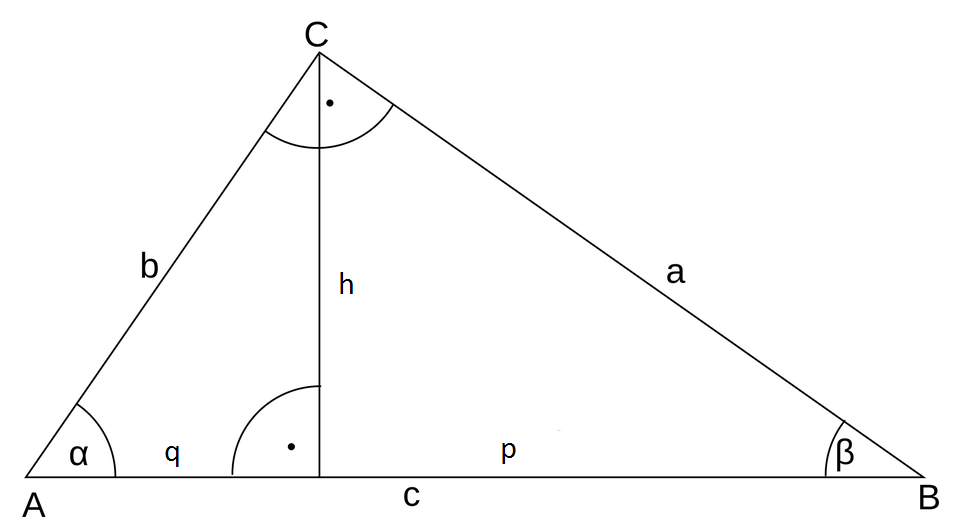
In the triangle ABC with $\gamma=90^\circ$ the altitude-on-hypotenuse theorem is:

$p\cdot c=a^2$

  • $a^2=p\cdot c$ $\Leftrightarrow$ $a=\sqrt{p\cdot c}$

  • $p=\frac{a^2}{c}$

  • $c=\frac{a^2}{p}$
such as

$q\cdot c=b^2$

  • $b^2=q\cdot c$ $\Leftrightarrow$ $b=\sqrt{q\cdot c}$

  • $q=\frac{b^2}{c}$

  • $c=\frac{b^2}{q}$