Divided areas between function graphs
A special case in the calculation of the area between function graphs is when the area is divided by an intersection into several subareas.
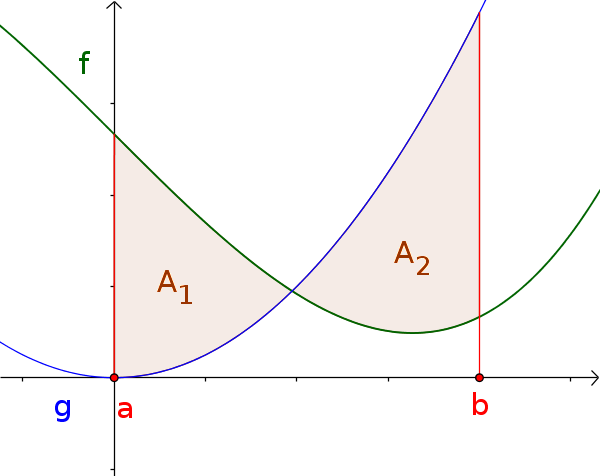
To the picture: The area $A_1$ is below $f$ and above $g$. The area $A_2$, however, is above $f$ and below $g$.
Due to the change, the areas must be calculated individually.
!
Remember
If one function is not consistently greater than the other over the entire interval, you must calculate the areas separately and then add them together.
This happens when the functions have an intersection within the interval.
This happens when the functions have an intersection within the interval.
i
Method
- Determine intersections and form intervals
- Find difference of the functions
- Calculate definite integrals for each interval
- Determine area
Example
Determine the area enclosed by the graphs of the functions $f(x)=\frac16x^3-x$ and $g(x)=-\frac16x^3+\frac13x^2+x$.
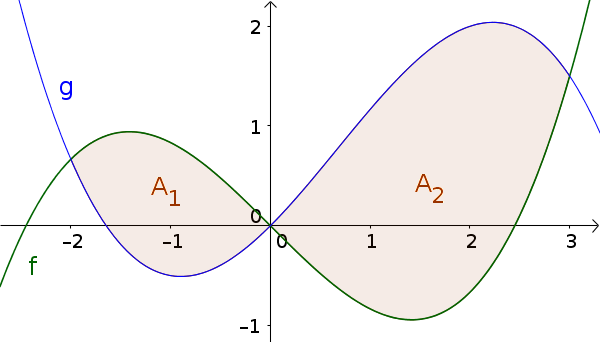
Hint: Enclosed area means the area between the outer intersections.
-
Determine intersections
Set functions equal to determine intersections.
$f(x)=g(x)$
$\frac16x^3-x=-\frac16x^3+\frac13x^2+x$
$\frac13x^3-\frac13x^2-2x=0$
$x\cdot(\frac13x^2-\frac13x-2)=0$
$x_{S_1}=0$
$\frac13x^2-\frac13x-2=0\quad|\cdot3$
$x^2-x-6=0$
(Solve quadratic equation, e.g. Quadratic formula I)
$x_{S_{2,3}}=\frac12\pm\sqrt{(\frac12)^2+6}$
$x_{S_2}=-2$ and $x_{S_3}=3$ -
Determine intervals
$x_{S_1}=0$ is between the two other intersection points and divides the area into two sections, which must be calculated individually.
$x_{S_1}=0$, $x_{S_2}=-2$ and $x_{S_3}=3$
$A_1$ over $[-2;0]$
$A_2$ over $[0;3]$ -
Difference of the functions
Subtract $g(x)$ from $f(x)$, combine and determine antiderivative.
$f(x)=\frac16x^3-x$
$g(x)=-\frac16x^3+\frac13x^2+x$
$h(x)=f(x)-g(x)$ $=(\frac16x^3-x)-$ $(-\frac16x^3+\frac13x^2+x)$ $=\frac13x^3-\frac13x^2-2x$
$H(x)=\frac{1}{12}x^4-\frac19x^3-x^2$ -
Find and calculate definite integrals
For both intervals, an integral must now be determined.
$\int_a^b (f(x)-g(x))\,\mathrm{d}x$ $=\int_a^b h(x)\,\mathrm{d}x$ $= [H(x) + C]_a^b$ $= H(b) - H(a)$
$A_1$ over $[-2;0]$
$\int_{-2}^0 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x$ $=[\frac{1}{12}x^4-\frac19x^3-x^2]_{-2}^0$ $=0-(\frac{1}{12}\cdot(-2)^4-\frac19\cdot(-2)^3-(-2)^2)$
$=0-(-\frac{16}{9})$ $=\frac{16}{9}$
$A_2$ over $[0;3]$
$\int_0^3 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x$ $=[\frac{1}{12}x^4-\frac19x^3-x^2]_0^3$ $=(\frac{1}{12}\cdot3^4-\frac19\cdot3^3-3^2)-0$
$=(-\frac{21}{4})-0$ $=-\frac{21}{4}$ -
Determine area
Now the area of each partition has to be determined and then added.
$A_1$ $=\int_{-2}^0 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x$ $=\frac{16}{9}$
$A_2$ $=|\int_0^3 (\frac13x^3-\frac13x^2-2x)\,\mathrm{d}x|$ $=|-\frac{21}{4}|$ $=\frac{21}{4}$
$A=A_1+A_2$ $=\frac{16}{9}+\frac{21}{4}\approx7.03$
