Math ↠ Application differential calculus ↠ Extreme value problem

Extreme value problem

One type of task that uses differential calculus are optimizations or extreme value problems. An extreme value problem is a kind of optimization problem but only with one constraint. It can be both a maximization problem and a minimization problem.

i

Hint

Extreme value problems exist when a target size (e.g., surface area, volume, profit, ...) is to become maximum or minimum. This condition is then the main condition.
!

Remember

In the case of extreme value problems, a function (the objective function) is set up from a main condition and a constraint, whose extreme values are searched for.
i

Method

  1. Main condition
  2. Constraint
  3. Set up objecitve function
  4. Calculate extreme values of the objective function
  5. Calculate missing sizes

Example

The largest possible rectangle area has to be limited with an 800 m fence. Calculate the size of both sides and the area.

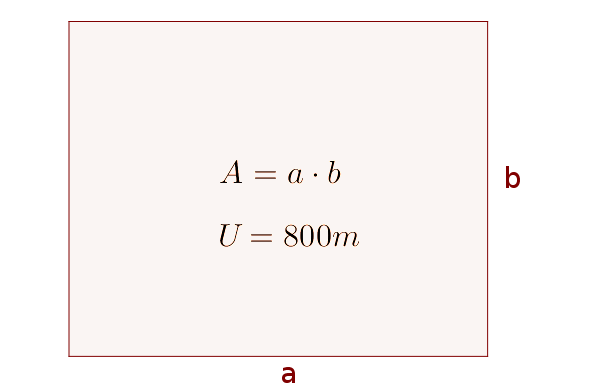
  1. Main condition

    The area of the rectangle should be maximized. Therefore, this is the main condition and depends on two variables $a$ and $b$.

    $A(a, b)=a\cdot b$

  2. Constraint

    There are only 800 m of fence available, which limits the area. This is the perimeter of the rectangle.

    $P=2a+2b$
    $800=2a+2b$

  3. Set up objective function

    To link both conditions, the constraint is changed to a variable.
    $800=2a+2b\quad|-2b$
    $800-2b=2a\quad|:2$
    $a=\frac{800-2b}2$ $=400-b$

    Now this must be used in the main condition and you get the objective function, which is dependent on only one variable.
    $A(a, b)=a\cdot b$
    $A(b)=(400-b)\cdot b$ $=400b-b^2$

  4. Calculate extreme values of the objective function

    Now you can (as with other functions too) calculate the extreme values of the objective function.
    $A(b)=400b-b^2$
    $A'(b)=400-2b$

    $400-2b=0\quad|-400$
    $-2b=-400\quad|:(-2)$
    $b=200$

    With the second derivation, it is still checked whether the result is actually a maximum point, since the area should be maximum.
    $A''(b)=-2$
    $A''(200)=-2<0$ => Maximum point

  5. Calculate missing sizes

    $b=200m$

    From the (converted) constraint you can now calculate $a$.
    $a=400-b$
    $a=400-200=200m$

    From the main condition (alternatively also with the objective function) the area $A$ can be calculated.
    $A(a, b)=a\cdot b$
    $A(a, b)=200m\cdot 200m=40.000m^2$