Inversely proportional relationship
Inversely proportional relationships are "the more the less"-relationships.
They always decrease evenly (proportional).
Example
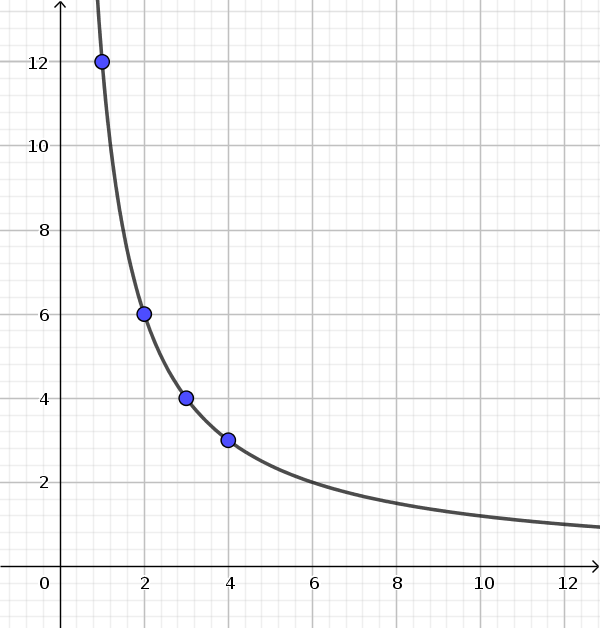
A worker needs 12 days. The number of days required decreases equally with increasing numbers of workers.
| Worker | needed days |
|---|---|
| 1 | 12 |
| 2 | 6 |
| 3 | 4 |
| 4 | 3 |
The graph is a hyperbola. It approaches the two axes more and more without reaching them.
!
Remember
If one doubles (triples, quadruples, ...) an initial value, the assigned value halves (thirds, quarters, ...).
Constant of inverse proportionality (total size)
If we multiply the assigned size times the initial size in an inversely proportional relationship, we always get the same value.
Example
| Worker | needed days |
|---|---|
| 1 | 12 |
| 2 | 6 |
| 3 | 4 |
| 4 | 3 |
$1\cdot12=\color{blue}{12}$
$2\cdot6=\color{blue}{12}$
$3\cdot4=\color{blue}{12}$
$4\cdot3=\color{blue}{12}$
The constant of inverse proportionality is here 12. It is therefore an inversely proportional relationship.
!
Remember
The constant of inverse proportionality or the total size is the product of initial value (x) and assigned value (y).
