Physik ↠ Quantentheorie ↠ Der lineare Potenzialtopf

Der lineare Potenzialtopf

Der lineare Potenzialtopf ist ein Modell eines quantenmechanischen Systems zur Beschreibung des Aufenthalts eines Teilchens.

Laut diesem Modell ist ein Teilchen zwischen zwei unendlich hohen Potenzialbarrieren eingeschlossen.

!

Merke

Unendlich hohe Potenzialbarriere bedeutet, dass zur Überwindung der Barriere eine unendlich hohe Energie notwendig wäre.

Aufbau des Modells

Es handelt sich um ein eindimensionales Modell, da sich das Teilchen nur in x-Richtung bewegen kann.

Potenzialtopf Modell

Folgende Eigenschaften gelten für das Modell:

  • Das Teilchen befindet sich ein einem Topf mit der Länge $L$

  • Die Energie innerhalb des Topfes beträgt:
    $E_{\rm{pot}}(x)=0$ für $0<x<L$

  • Die Ränder stellen die unendlich hohen Potenzialbarrieren dar:
    $E_{\rm{pot}}(x)=0$ für $x<0$ und $x>L$

Stehende Wellen

Die Teilchen können sich nur zwischen den beiden Barrieren aufhalten.

Damit dies möglich ist, müssen ihre Wellenlängen allerdings so sein, dass sie sich nicht selbst weginterferieren. Sie müssen also eine stehende Welle ausbilden.

i

Tipp

Stehende Wellen haben die Eigenschaft, dass die Auslenkung an bestimmten Stellen immer bei Null verbleibt. Diese Stellen nennt man Wellenknoten und sind in unserem Modell zum Beispiel immer an den Rändern zu finden.

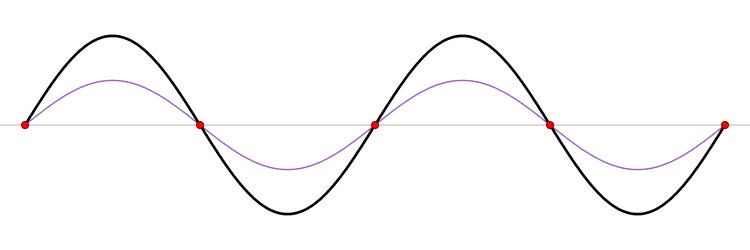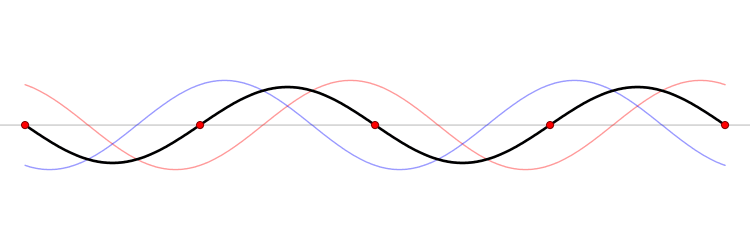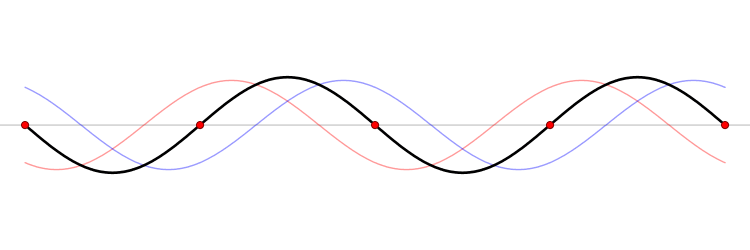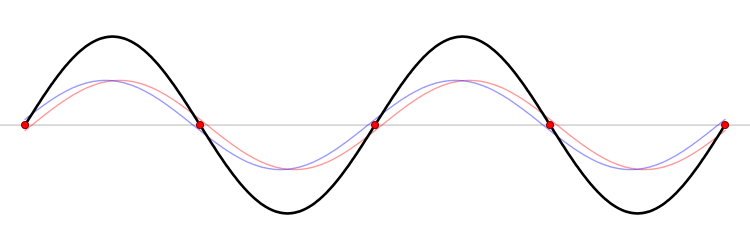
Beispiel einer stehenden Welle (schwarz) und der Knotenpunkte (rot) Stehende Welle
!

Merke

Bei stehenden Wellen gilt für den Zusammenhang von Wellenlänge $\lambda$ und Länge $L$:

$L=\frac{\lambda}2\cdot n$

Und damit auch

$\lambda = \frac{2L}{n}$
Linearer Potenzialtopf

Energiewerte des Teilchens

Die Teilchen im Potenzialtopf können nur bestimmte diskrete Energieniveaus annehmen.

Herleitung

Die Energie des Teilchens entspricht seiner kinetischen Energie, da die potentielle Energie ja Null sein soll. Die Formel lässt sich dann mit Hilfe von $p=mv$ bzw. $p^2=m^2 v^2$ (siehe Impulse) weiter umformen.

$E = \frac{1}{2} m \cdot v^2 $ $= \frac{p^2}{2m}$


Nach De-Broglie gilt für die Wellenlänge

$\lambda = \frac{h}{p} \Rightarrow p=\frac{h}{\lambda}$



Einsetzen der Bedingung für stehende Wellen:

$p=\frac{h}{2L} \cdot n$

Schließlich erhalten wir für die Energie unseres Teilchens

$E= \frac{h^2}{8L^2m}\cdot n^2$

mit $n=1,2,3,...$