Zentripetalbeschleunigung

Wie bereits erwähnt wirkt bei gleichförmigen Kreisbewegungen eine Kraft auf die Masse. Diese Kraft beschleunigt die Masse in Richtung des Zentrums. Die Beschleunigung nennt sich Zentripetalbeschleunigung.
Doch wie wird sie berechnet?

Wie für jede andere Beschleunigung gilt:

$a_Z=\frac{\Delta v}{\Delta t}$

Wir suchen nun also eine Geschwindigkeits- und eine Zeitänderung. Dies zeigen wir am besten an einem Schaubild.

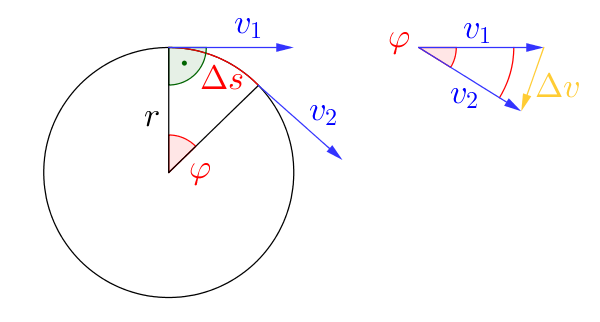
Man erkennt, dass die Geschwindigkeitsveränderung $\Delta v$ etwa so lang ist, wie der Kreisbogen an der gleichen Stelle. Wird das Zeitintervall kleiner, so nährt sich der Wert weiter an.
Daher gilt:

$\Delta v=\varphi\cdot v_1$

oder (umgestellt):

$\varphi=\frac{\Delta v}{v_1}$

Außerdem gilt, wie auf dem linken Teil des Schaubildes sichtbar, dass $\Delta s$ im Verhältnis zu $\varphi$ und $r$ steht.

$\varphi=\frac{\Delta s}{r}$

Durch Gleichsetzen erhalten wir eine Abhängigkeit zwischen Radius, zurückgelegter Strecke und Geschwindigkeit:

$\frac{\Delta s}{r}=\frac{\Delta v}{v}$

Wir haben ein $\Delta v$ in unserer Gleichung, es fehlt aber noch ein $\Delta t$. Um dieses zu erhalten, rechnen wir es einfach beidseitig hinzu. Dafür teilen wir durch $\Delta t$.

$\frac{\Delta s}{r}=\frac{\Delta v}{v}\quad|:\Delta t$

$\frac{\Delta s}{r\cdot\Delta t}=\frac{\Delta v}{v\cdot\Delta t}$

Nun haben wir beide notwendigen Variablen. Wir können die Gleichung mit Hilfe zweier Formeln umstellen.

$a=\frac{\Delta v}{\Delta t}$ einsetzen in $\frac{\Delta s}{r\cdot\Delta t}=\frac{\Delta v}{v\cdot\Delta t}$

$\frac{\Delta s}{r\cdot\Delta t}=\frac{a}{v}$

$v=\frac{\Delta s}{\Delta t}$ einsetzen in $\frac{\Delta s}{r\cdot\Delta t}=\frac{a}{v}$

$\frac{v}{r}=\frac{a}{v}$

Zuletzt stellen wir die Formel noch nach a um.

$a_Z=\frac{v^2}{r}$