Was hält die Masse auf Kurs?

Bei gleichförmigen Kreisbewegungen bleibt der Betrag der Geschwindigkeit stets gleich. Allerdings ändert sich die Richtung der Bewegung ständig. Sie ist immer rechtwinklig zum Radius und verläuft entlang der Kreisbahn. Daher muss irgendetwas die Bewegung verändern.

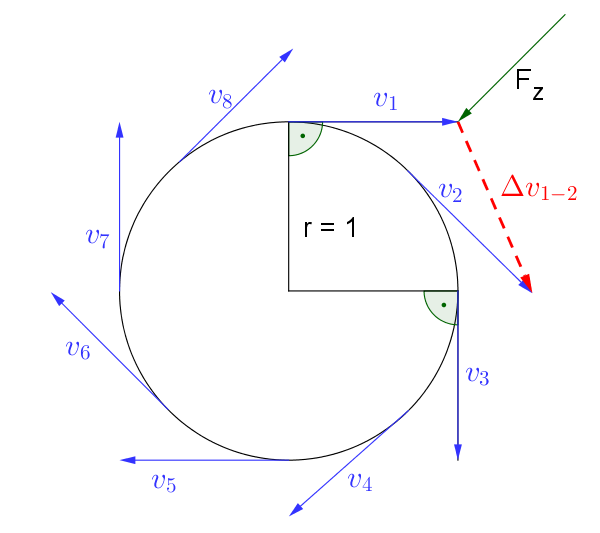
Wie im Schaubild gut sichtbar ist, verändert sich die Geschwindigkeit $v_1$ zu $v_2$ hin stark. Um diese Einwirkung zu erklären, bleibt nur eine Möglichkeit: Eine Kraft wirkt auf die Masse und ändert so ihre Richtung. Diese Kraft wird die Zentripetalkraft genannt. Sie wirkt entlang des Radius zum Zentrum hin und wird wie andere Kräfte definiert:

Diese Werte sind berechenbar und werden in den folgenden Themen erklärt.