Winkelgeschwindigkeit

Bei Kreisen gibt es mehrere Geschwindigkeiten, die Bahngeschwindigkeit und die Winkelgeschwindigkeit. Um den Unterschied zwischen den beiden besser verstehen zu können, schauen wir uns ein Beispiel an.

Beispiel

Die Erde dreht sich als Kugel einheitlich schnell im Kern. Allerdings hat sie außen am Äquator eine viel höhere Geschwindigkeit als an den Polen. Das liegt daran, dass der Radius größer ist. Um nun aber eine einheitliche Geschwindigkeit der Erde angeben zu können nutzt man die Winkelgeschwindigkeit $\omega$

Im Unterschied zur Geschwindigkeit $v$ definiert sich die Winkelgeschwindigkeit aus Winkeländerung pro Zeit.

Wiederholung

$v=\frac{\Delta s}{\Delta t}$

$\text{Geschwindigkeit}=\frac{\text{Strecke}}{\text{Zeit}}$

$\omega=\frac{\Delta \varphi}{\Delta t}$

$\text{Winkelgeschwindigkeit}=\frac{\text{Winkeländerung}}{\text{Zeit}}$

Der Winkel der Winkelgeschwindigkeit wird im Bogenmaß gemessen. Um nun die Winkelgeschwindigkeit zu bestimmen, wird die Veränderung des Winkels im Bogenmaß und eine dazugehörige Zeit benötigt. Sie wird dann in $\frac1s$ angegeben.

Beispiel

Ein Uhrzeiger braucht für eine halbe Runde auf der Uhr 30 Sekunden.

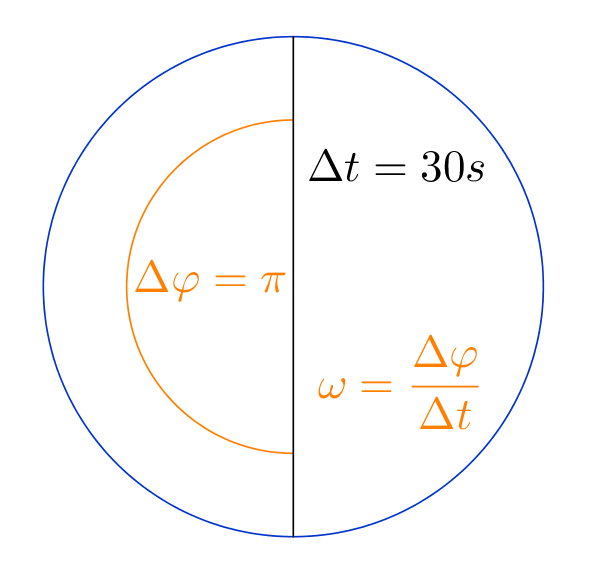
Die Winkeländerung bei einer halben Runde beträgt $\pi$.
Daraus folgt:

$\omega=\frac{\Delta \varphi}{\Delta t}$

$\omega=\frac{\pi}{30s}$

$\omega=\frac{\pi}{30} \frac1s$

Merke

Da eine Runde im Bogenmaß $2\pi$ hat und sich die Zeit für einen Umlauf $T$ berechnen lässt, kann man eine allgemeine Formel aufstellen.

$\omega=\frac{2\pi}{T}$

$\text{Winkelgeschwindigkeit}$ $=\frac{\text{Runde im Bogenmaß}}{\text{Zeit für eine Runde}}$

Info

Auch möglich ist eine Formel mit der Frequenz $f=\frac1T$:

$\omega=2\pi\cdot f$

$\text{Winkelgeschwindigkeit}$ $=\text{Runde im Bogenmaß}\cdot \text{Frequenz}$